A geometry problem by George G

Geometry Level 3

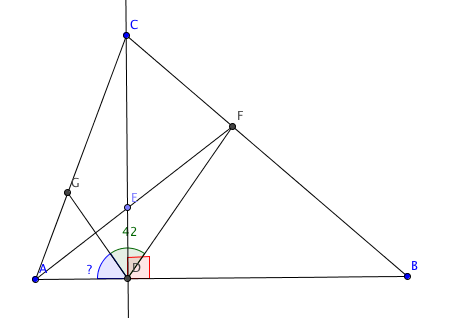
In scalene triangle ABC, let E be a point on altitude CD. AE and BE meet sides CB and CA at points F and G, respectively. If $\angle{FDG} = 42^{\circ}$ , what is the measure (in degrees) of $\angle{ADG}$ ?

The answer is 69.

11 solutions

Anh Tuong Nguyen
Dec 26, 2013

We can use harmonic division to solve this problem.

Let H and I be the intersection of GF with CD and AB, respectively. By harmonic division, since AF, BG and CD are concurrent, (IADB) is harmonic. Also, since AG, DE and BF are concurrent, (IGHF) is also harmonic.

However, we also have $\angle HDI = 90^\circ$ , hence DH is the bisector of $\angle GDF$ . Therefore $\angle GFC=21^\circ$ and $\angle ADG = 69^\circ$ .

Anyone unfamiliar with harmonic division can search for the PDF article called 'Harmonic Division and its application' by Cosmin Pohoata, all the results that I used here can be found within the first 2 pages. It is a very powerful tool to solve geometry problems.

I also done like this. its soo easy

Arvind Jilla - 7 years, 3 months ago

Faraz Masroor
Dec 24, 2013

By blanches theorem (can be proven with harmonic divisions or by drawing a line through C parallel to AB, extending AE and BE to hit the line, ceva and congruence) that Angle cdg=cdf. Answer follows.

Gokul Krish
Jun 8, 2014

angle HDI =90 angle GFC=21 so,90+21-180=angle ADG=69

Muhammad Azam
Mar 19, 2014

angle ADG+GDF+FDB=180
angle ADG= angle FDB
180-42=138
ADG+FDB=138
ADG+ADG=138
2ADG=138
angle ADG =138/2= 69

How angle ADG is equal to Angle FDB

Archiet Dev - 7 years ago

This is a kind of theorem which is proved by vertically opposite angles.

Mehul Arora - 6 years, 7 months ago

Lecher Maningo
Mar 13, 2014

42/2=21 so i subtract it to 90-21=69

Sonu Singh
Feb 25, 2014

As , < ADG + <GDE + <EDF +<FDB =180 degree --------------------------------(1) so,< < ADG+ <FDB =138 degree --------------------------------(2) let,AE and DG intersect each other at T <GDA+<GDE=90 degree-----------------------------------(3) Eqn(1) - Eqn(2), we get, <AED - <GDE =48 degree -----------------(4) also ,in triangle AED, <EAD+<DEA=90 degree --------------------(5) also , in triangle TAD ,<ATD= <EAD+<DEA=90 degree ( exterior angle is equal to sum of interior opposite angle) <EAD+<DEA=90 degree ---------------------------------------(6) subtracting Eqn.(4) -Eqn. (6) , we get <AED =69 degree so <GDE=21 Degree But, <ADE= <ADG+<GDE=90 Degree , putting value of <GDE WEe get, <ADG=69 Degree , as required

Badagha Jivan
Feb 24, 2014

hd is bisector of angle gdf. now it is simple.

Jatinder Singh
Jan 21, 2014

as altitudes are concurrent, therefore BG,AF are altitudes as well.so construct those altitudes. we can see that pts ADEG are concyclic as well as pts BDEF , CFEG.as given angle of pedal triangle is 42=180-2C . so C=69 deg.
As pts CGEF are concyclic so angle GEF = 180-69, so angle GEA=69 . As pts GEDA are also concyclic so angle GEA=angle GDA=69 deg.

Raven Herd
Jan 17, 2014

angle FDG is divided into 2 by the perpendicular CD i.e 42/2= 21. That implies angle EDG is 21.The angle CDAis 90 {as it is perp.} therefore,angle ADG = CDA - CDG= 90 - 21= 69

Marcos Oliveira
Dec 29, 2013

<EDG = $\frac{42}{2}$ = 21
<EDA = 90
<EDA - <EDG = <ADG ----------> <ADG = 90 - 21 = $\boxed{69}$

can you tell why angleEDG = 2 ANGLE EDG

vaishnav garg - 7 years, 4 months ago

I will go with this solution

Sudha Menon - 7 years, 3 months ago

GOOD

muhammad azam - 7 years, 2 months ago

Budi Utomo
Dec 26, 2013

90-(42/2) = 90 - 21 = 69

How did you get this?

minimario minimario - 7 years, 5 months ago

Set $\widehat{CDF}=x,\widehat{CDG}=y$ We have $\frac{BF}{CF}=\frac{BD\cos x}{CD\sin x}$ $\Rightarrow \tan x=\frac{BD.CF}{BF.CD}$ Similarly $\tan y=\frac{CG.AD}{AG.CD}$ By Ceva's theorem,we have $AD.BF.CG=BD.CF.AG$ So $\tan x=\tan y$ .But $0<x,y<90^{\circ}$ , then x=y

Huy Pham - 7 years, 5 months ago

But why Bf=Bd Cosx

Rajat Raj - 7 years, 4 months ago

A geometry problem by George G

The answer is 69.

11 solutions

0 pending reports