An interesting problem about circle
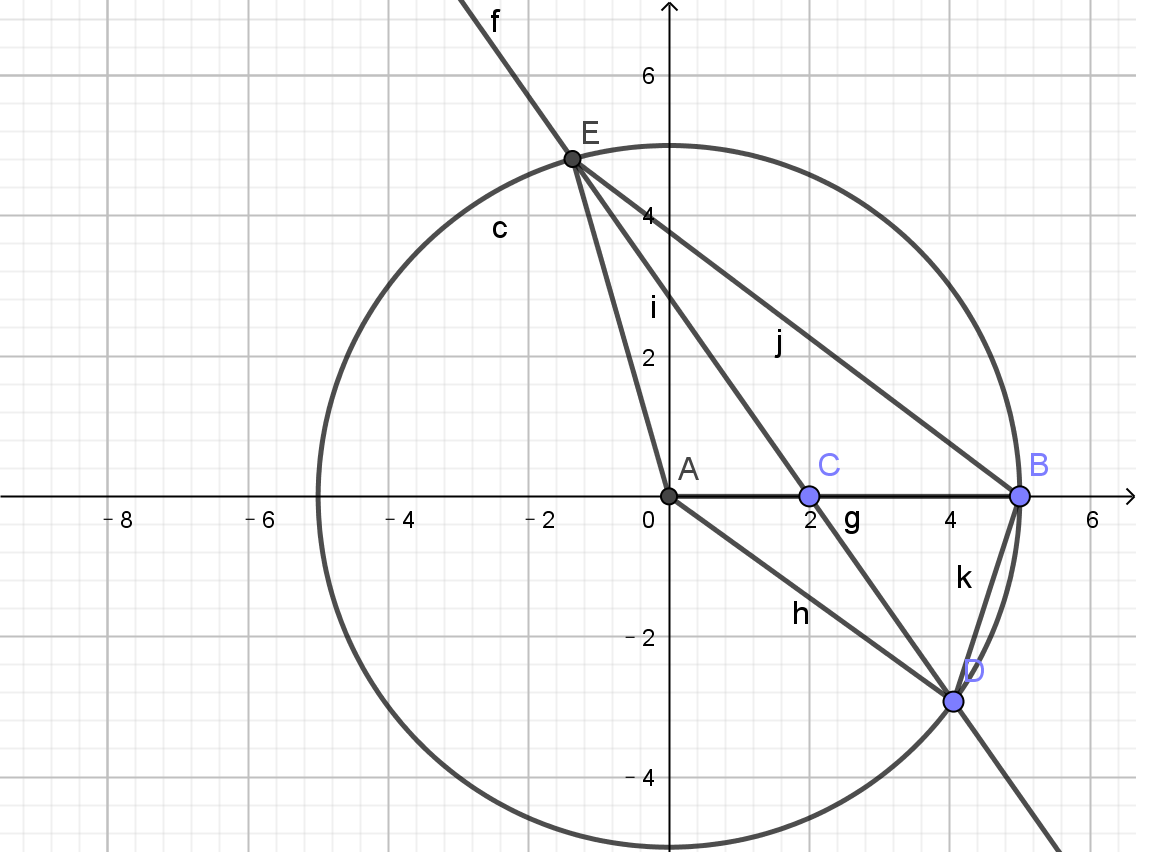 There are fixed points C and B in a circle A. AC = 2, BC = 3. D is a moving point on the circle. E is the intersection point of the circle and the line CD. As D moves on circle, the value of tan∠BED * tan∠BDE stays the same.So what is the value?
(accurate to 4 decimal places)
There are fixed points C and B in a circle A. AC = 2, BC = 3. D is a moving point on the circle. E is the intersection point of the circle and the line CD. As D moves on circle, the value of tan∠BED * tan∠BDE stays the same.So what is the value?
(accurate to 4 decimal places)
I know the value, but I don't know why!
The answer is 0.4286.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The Intersecting Chords Theorem tells us that C D × C E = C B × C F = 3 × 7 = 2 1 and hence tan θ tan ϕ = C D × C E 9 = 7 3