An interesting trajectory
A particle describes a path (see the figure below) which in polar coordinates is given by the equation r 2 = R 2 cos ( 2 θ ) . It turns out that such trajectory is possible when the particle moves under the influence of a central force of the form F ( r ) = r n C where C is a constant, r is the distance to the origin O and n is an integer. Determine n .
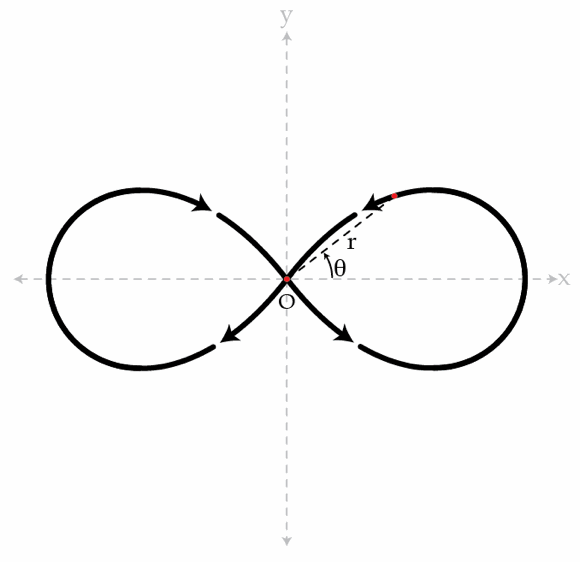
Note that a central force is always directed toward a fixed point (point O in this case).
Details and assumptions
- Consider only one half of the diagram, i.e. the particle travels around the left lobe or the right lobe, but not both.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
In planar polar coordinates, the radial and transverse components of acceleration are r ¨ − r θ ˙ 2 and r θ ¨ + 2 r r ˙ θ ˙ = r 1 d t d ( r 2 θ ˙ ) . Thus, for a particle of mass m in an attractive central field of magnitude F ( r ) = r n C , we have r ¨ − r θ ˙ 2 = − m C r − n h = r 2 θ ˙ where h is constant, the angular momentum per unit mass.
If we change variables, and consider u = r − 1 , then r ˙ r ¨ = = − u − 2 d θ d u θ ˙ = − h d θ d u − h d θ 2 d 2 u θ ˙ = − h 2 u 2 d θ 2 d 2 u so that the differential equation becomes − h 2 u 2 d θ 2 d 2 u − h 2 u 3 d θ 2 d 2 u + u = = − m C u n m h 2 C u n − 2 The trajectory r 2 = R 2 cos 2 θ leads to u d θ d u d θ 2 d 2 u d θ 2 d 2 u + u = = = = = = = R − 1 ( sec 2 θ ) 2 1 R − 1 2 1 ( sec 2 θ ) − 2 1 × 2 sec 2 θ tan 2 θ R − 1 ( sec 2 θ ) 2 1 tan 2 θ R − 1 ( sec 2 θ ) 2 1 tan 2 2 θ + 2 R − 1 ( sec 2 θ ) 2 1 sec 2 2 θ R − 1 [ tan 2 2 θ + 2 sec 2 2 θ ] ( sec 2 θ ) 2 1 R − 1 [ tan 2 2 θ + 1 + 2 sec 2 2 θ ] ( sec 2 θ ) 2 1 R 3 ( sec 2 θ ) 2 5 = 3 R 4 u 5 and so this trajectory is possible provided that n = 7 .
Suppose that the particle did try to follow this path, and assume that θ = 0 when t = 0 . Since R 2 cos 2 θ θ ˙ = h , we deduce that sin 2 θ = R 2 2 h t 0 ≤ t ≤ 2 h R 2 and hence r = ( R 4 − 4 h 2 t 2 ) 4 1 0 ≤ t ≤ 2 h R 2 Chasing the formulae, the speed of the particle at any point is v = R 2 h ( R 4 − 4 h 2 t 2 ) − 4 3 Thus, in a finite time 2 h R 2 the particle attains infinite speed and reaches the origin, where it presumably has a fairly satisfying collision with the source of the central force. It strikes me as unlikely that the particle will survive to make it into the left-hand half of the curve!
Reference: See for example David Morin's book on Classical Mechanics.
First note that the force law F ( r ) = C / r n , C < 0 , implies that the potential is V ( r ) = − n r n − 1 C ≡ r n − 1 B such that F ( r ) = − d r d V ≡ − V ′ ( r ) .
For central forces, acceleration is only along the radial direction. The tangential part is zero. The radial and tangential accelerations of a point mass in polar coordinates are a r = r ¨ − r θ ˙ 2 ; a θ = 2 r ˙ θ ˙ + r θ ¨ = 0 . The second equation results in the conservation of angular momentum L and it allows us to express angular velocity in terms of L : L = m r 2 θ ˙ = Const. ⇒ θ ˙ = m r 2 L The Newton's law can now be expressed as m a r = m r ¨ − m r 3 L = F ( r ) = − V ′ ( r ) . This equation can be integrated once (after multiplication with r ˙ ) to yield conservation energy equation: 2 1 m r ˙ 2 + 2 m r 2 L + V ( r ) = E .
Noting that r ˙ = d θ d r θ ˙ = d θ d r m r 2 L , the conservation energy equation can be transformed into ( r 2 1 d θ d r ) 2 + r 2 1 = L 2 2 m E − L 2 2 m V ( r ) . Given r 2 ( θ ) = R 2 cos ( 2 θ ) , and noting that r d θ d r = − R 2 sin ( 2 θ ) , and substituting this into the last differential equation, we get r 6 R 4 = L 2 2 m E + L 2 2 m V ( r ) . Comparing the equations, it is evident that E = 0 , and n = 7 .
A typo: In the first equation, the expression for V ( r ) should not contain a " − " sign: V ( r ) = n r n − 1 C ≡ r n − 1 B . . . and so on Another typo: In the conservation of energy equation and the equation above, there should have been L 2 instead of L . Here are corrected equations:
The Newton's law can now be expressed as m a r = m r ¨ − m r 3 L 2 = F ( r ) = − V ′ ( r ) . This equation can be integrated once (after multiplication with r ˙ ) to yield conservation energy equation: 2 1 m r ˙ 2 + 2 m r 2 L 2 + V ( r ) = E .
Simplest solution from elementry concepts
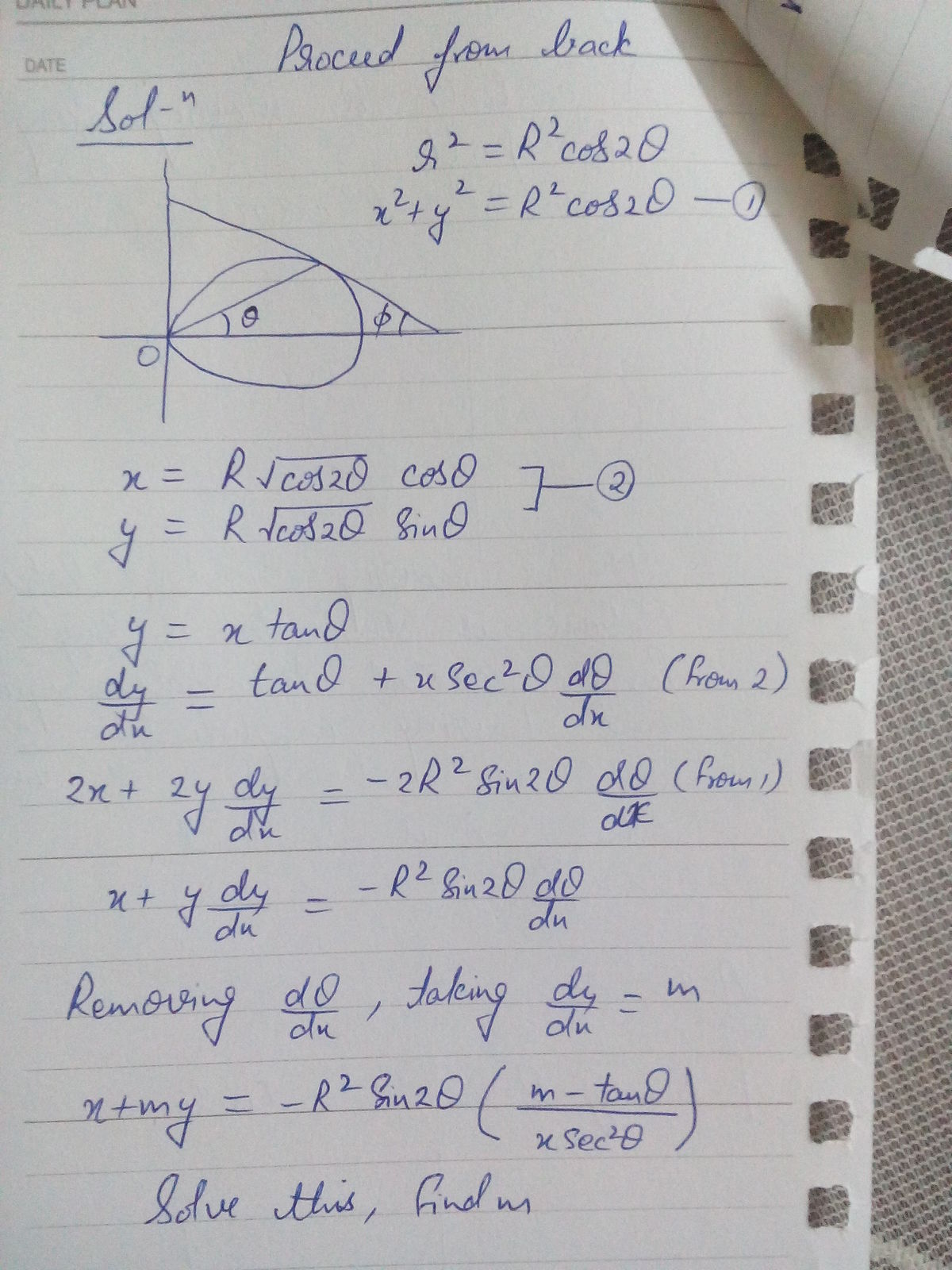


I think it is motivated by the above solutions but presented in a basic way
Log in to reply
Well, talking frankly... I didn't get most of the above solutions for I don't know anything about Binet's equation.
And yes, it was my motive to present solution in a basic way so that everyone can understand it.
We can see this as a classical central-force problem, and thus apply the Binet's equation to solve this problem. Before we begin solving the problem, a brief overview of the derivation of the equation is as follows: we know that particles moving under a central force experience no change in angular momentum, since the central force only acts in the radial component of the acceleration of the particle [for the full mathematical proof, look here ]. So we can let h be the specific angular momentum of the particle (which is the angular momentum of the particle divided by its mass m ), where h is a constant. Now, if we let u = r 1 be the reciprocal of the distance from the origin, then we can write the central force in terms of u using Binet's formula: F ( u ) = − m h 2 u 2 ( d θ 2 d 2 u + u ) [for the full mathematical proof, look here ].
So first, we need to determine what d θ 2 d 2 u is.
r 2 = R 2 cos ( 2 θ ) u 2 1 = R 2 cos ( 2 θ ) d θ d ( u 2 1 ) = d θ d [ R 2 cos ( 2 θ ) ] u 3 1 d θ d u = R 2 sin ( 2 θ ) d θ d u = u 3 R 2 sin ( 2 θ ) d θ 2 d 2 u = R 2 u 3 [ 2 cos ( 2 θ ) ] + R 2 sin ( 2 θ ) ( 3 u 2 d θ d u ) = 2 u 3 [ R 2 cos ( 2 θ ) ] + 3 u 5 R 2 sin ( 2 θ ) ( u 3 1 d θ d u ) = 2 u 3 ( u 2 1 ) + 3 u 5 R 2 sin ( 2 θ ) [ R 2 sin ( 2 θ ) ] = 2 u + 3 u 5 R 4 sin 2 ( 2 θ ) = 2 u + 3 u 5 R 4 [ 1 − cos 2 ( 2 θ ) ] = 2 u + 3 u 5 R 4 − 3 u 5 R 4 cos 2 ( 2 θ ) = 2 u + 3 u 5 R 4 − 3 u 5 [ R 2 cos ( 2 θ ) ] 2 = 2 u + 3 u 5 R 4 − 3 u 5 ( u 2 1 ) 2 = 2 u + 3 u 5 R 4 − 3 u = 3 u 5 R 4 − u
So now we substitute this back into the Binet's equation to obtain
F ( u ) = − m h 2 u 2 ( d θ 2 d 2 u + u ) = − m h 2 u 2 ( 3 u 5 R 4 − u + u ) = − m h 2 u 2 ( 3 u 5 R 4 ) = − 3 R 4 m h 2 u 7 .
Since r = u 1 , then we can substitute this back into the expression above to get
F ( r ) = F ( u 1 ) = − 3 R 4 m h 2 ( u 1 ) 7 = u 7 − 3 R 4 m h 2 = u 7 C , where C = − 3 R 4 m h 2 is a constant.
Therefore, n = 7 .