An Interesting Triangle

Extend AI to meet the circle in M, the midpoint of smaller arc BC. Further, Join M to O and produce it to meet the circumcircle in N. Let the in-circle touch AB in L. From M draw a perpendicular to BC meeting the latter in P. Now we can see that Tr. AIL///Tr. NBM; AI MB=IL NM=2r R. We further observe that MP=r since GI//BC and thus r/MB=sin(A/2) as also r/AI=sin(A/2) which implies that AI=MB & therefore AI²=2r R. We now recall by Euler's Formula : OI²=R² -2r*R or OI²=R²-AI² or AI²+OI²=R² or /_OIA =90° by the converse of Pythagoras Theorem.

This proof is incomplete and I would be grateful if someone can establish why MP = r

Let $M$ be the point where the angle bisector $AE$ meets the circumcircle of $\triangle ABC$ when extended. Then, $M$ is the midpoint of $\overset\frown{BC}$ and line $OM$ is the perpendicular bisector of $BC$ , hence, the point of intersection of $OM$ and $BC$ is the midpoint $P$ of $BC$ .
Let, also, $D$ be the point of tangency of the incircle with side $BC$ . Finally, denote $AB$ by $c$ , $BC$ by $a$ and $CA$ by $b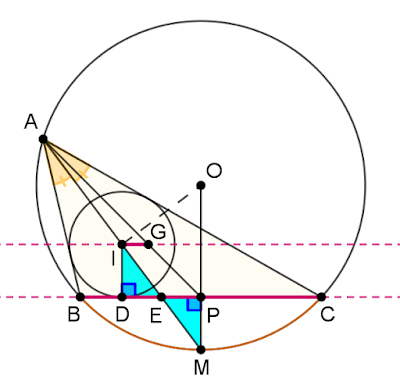$ . The claim is that $\angle AIO=90{}^\circ$ .

To prove it, we just have to show that $OI$ is the apothem of chord $AM$ , or, equivalently, that $I$ is the midpoint of $AM$ .
Further down we‘ll use the following formulae:

Distance of the incenter from a vertex $AI=\frac{b+c}{a+b+c}\cdot AE \ \ \ \ \ (1)$ $BE=\dfrac{ac}{b+c} \ \ \ \ \ (2)$ $BD=s-b=\dfrac{a-b+c}{2} \ \ \ \ \ (3)$ where $s$ is the semiperimeter of $\triangle ABC$ , i.e. $s=\frac{a+b+c}{2}$ .

Since $IG$ is parallel to $BC$ , we have

$\dfrac{AI}{AE}=\dfrac{AG}{AP}\overset{(1)}{\mathop{\Rightarrow }}\,\dfrac{b+c}{a+b+c}=\dfrac{2}{3}\Rightarrow b+c=2a \ \ \ \ \ (4)$ .

Now, $DE=BE-BD\overset{(1),(2),(3)}{\mathop{=}}\,\frac{ac}{b+c}-\frac{a-b+c}{2}\overset{(4)}{\mathop{=}}\,\frac{c\frac{b+c}{2}}{b+c}-\frac{\frac{b+c}{2}-b+c}{2}=\frac{b-c}{4} \ \ \ \ \ (5)$ On the other hand, $EP=BP-BE\overset{(2)}{\mathop{=}}\,\frac{a}{2}-\frac{ac}{b+c}\overset{(4)}{\mathop{=}}\,\frac{\frac{b+c}{2}}{2}-\frac{\frac{b+c}{2}c}{b+c}=\frac{b-c}{4} \ \ \ \ \ (6)$

$\left( 5 \right),\left( 6 \right)\Rightarrow DE=EP$ .

This implies that the blue right angled triangles $\triangle IDE$ and $\triangle MPE$ are congruent, thus, $IE=EM$ .

We have reached our goal, since

$\dfrac{AI}{AE}=\dfrac{2}{3}\Rightarrow AI=2IE=IE+EM=IM$ , i.e. $I$ is indeed the midpoint of $AM$ Q.E.D.

Note: Please, ask if you want me to include a proof of formula $(1)$ , or any other.