An interior point with a special property

Geometry Level 3

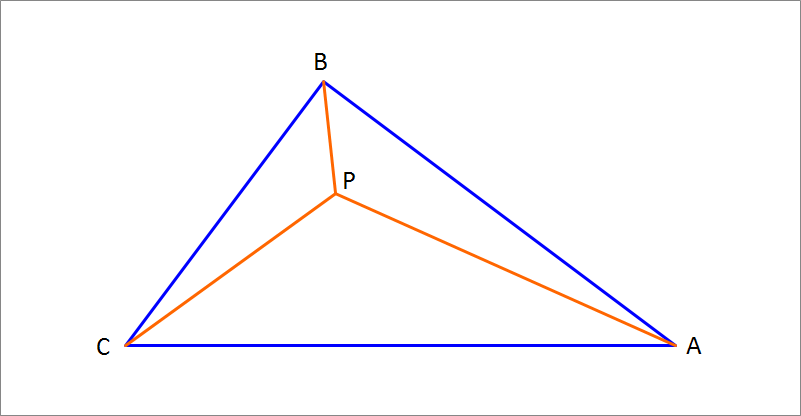
$\triangle ABC$ is a right triangle at $B$ , and has $AB = 4$ , $BC = 3$ , $AC = 5$ . You want to place a point $P$ inside the triangle, such that $\angle APB = \angle BPC = \angle CPA = 120^{\circ}$ , as shown in the attached figure.

Find this point and submit as your answer $\lfloor 100(AP + BP + CP) \rfloor$ , where $\lfloor \cdot \rfloor$ is the floor function (for example $\lfloor 3.4 \rfloor = 3$ ).

The answer is 676.

1 solution

Ajit Athle
Aug 9, 2018

I) What we want is the first Fermat Point (P) of the triangle and this can be determined as shown in the diagram by drawing outward equilateral triangles on AB & BC.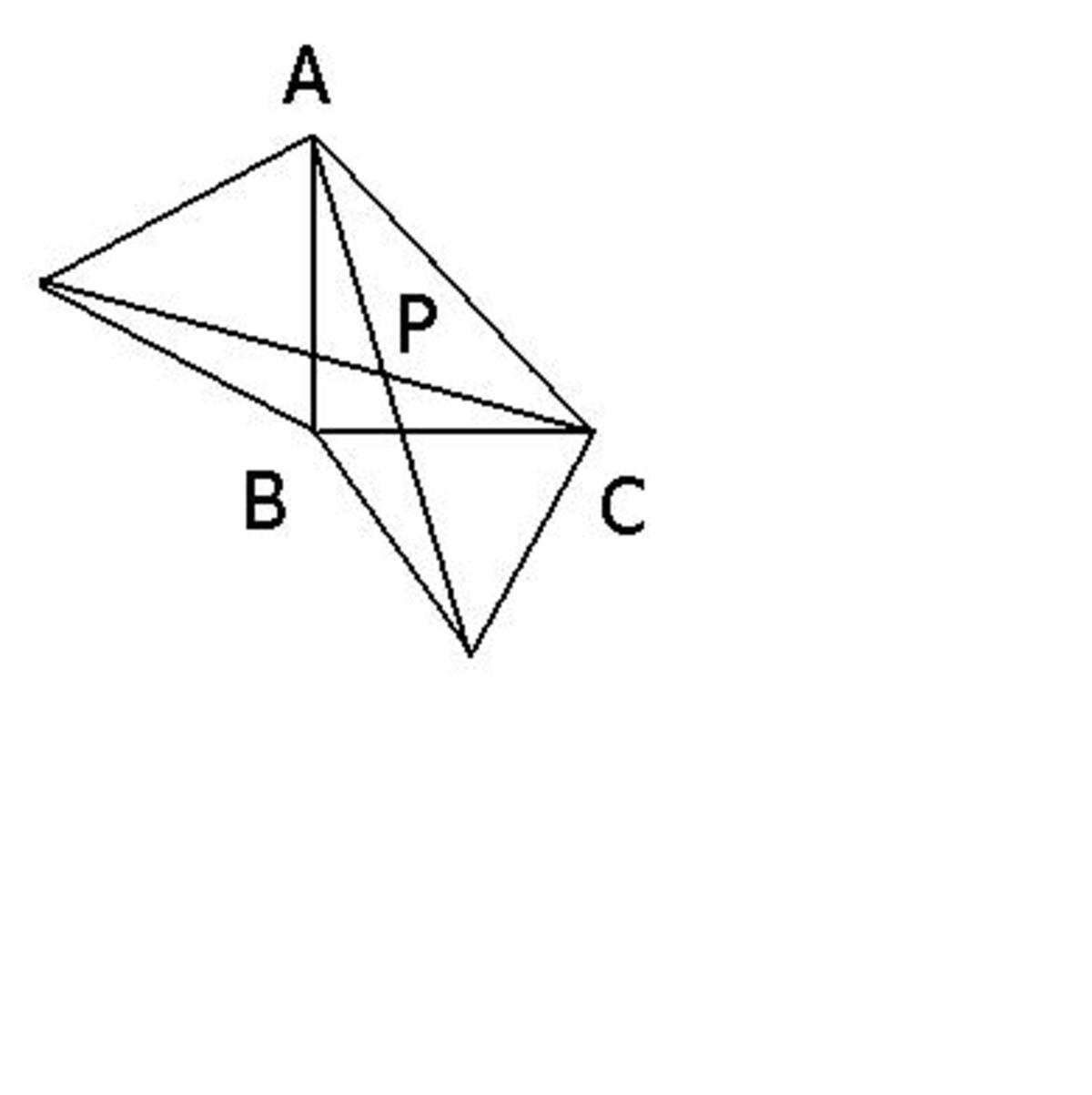 Point P turns out to be the intersection of the following two lines: y=(6-2x)/(3+2(3)^(1/2)) and y=4 - (8+3(3)^(1/2))x/3. As a matter of fact, P:( 0.75118,0.69579). The required expression can now be calculated using the distance formula. II) Since the Fermat Point is such that / CPA=/ APB=/_BPC=120°, we can write the following equations: a²+b²+ab=9, a²+c²=16, b²+c²=25 which yiels a=1.02391, b=2.354 & c=3.38852 with the Reqd. Expression =100(a+b+c)=676.643

An interior point with a special property

The answer is 676.

1 solution

0 pending reports