An Irregular Pentagram

The pentagram has four vertex angles of $30^\circ$ and one vertex angle of $60^\circ$ . Its inner pentagon is made up of four congruent right-angled triangles with perpendicular sides of lengths $\tfrac12$ and $\tfrac{1}{2\sqrt{3}}$ , and hence the pentagon has area $4 \times \tfrac12 \times \tfrac12 \times \tfrac{1}{2\sqrt{3}} \; = \; \frac{\sqrt{3}}{6}$ making the answer $3+6 = \boxed{9}$ .

Since the sum of two sets of exterior angles of the interior pentagon is $2 \cdot 360° = 720°$ , and the sum of the angles of the five triangles around it is $5 \cdot 180° = 900°$ , the angle tips have a sum of $900° - 720° = 180°$ .

Letting $x$ be the measurement of one of the four congruent angle tips, the fifth angle tip is $2x$ , which means $4x + 2x = 180°$ , so that $x = 30°$ . Therefore, the five angle tips are $30°$ , $30°$ , $30°$ , $30°$ , and $60°$ .

Let the pentagram be labelled as follows:

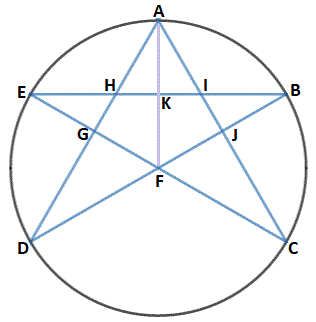
By symmetry, since $\angle DAC = 60°$ , then $\angle FAC = 30°$ . By the inscribed angle theorem, since $\angle ADB = 30°$ , then $\angle AFB = 60°$ . As radii, $AF = BF = 1$ . Solving $\triangle AFJ$ , $\angle AJF = 90°$ , $FJ = \frac{1}{2}$ , and $AJ = \frac{\sqrt{3}}{2}$ , and solving $\triangle BKF$ , $\angle BKF = 90°$ and $KF = \frac{1}{2}$ , and solving $\triangle AKI$ , $AK = AF - KF = \frac{1}{2}$ and $KI = \frac{\sqrt{3}}{6}$ .

The area of $\triangle AFJ$ is then $A_{\triangle AFJ} = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{8}$ , and the area of $\triangle AKI$ is then $A_{\triangle AKI} = \frac{1}{2} \cdot \frac{\sqrt{3}}{6} \cdot \frac{1}{2} = \frac{\sqrt{3}}{24}$ .

By symmetry, the area of the inner pentagon is $A_{FGHIJ} = 2 (A_{\triangle AFJ} - A_{\triangle AKI}) = 2(\frac{\sqrt{3}}{8} - \frac{\sqrt{3}}{24}) = \frac{\sqrt{3}}{6}$ .

Therefore, $p = 3$ , $q = 6$ , and $p + q = \boxed{9}$ .