An oblique cut on a cuboid
Geometry
Level
3
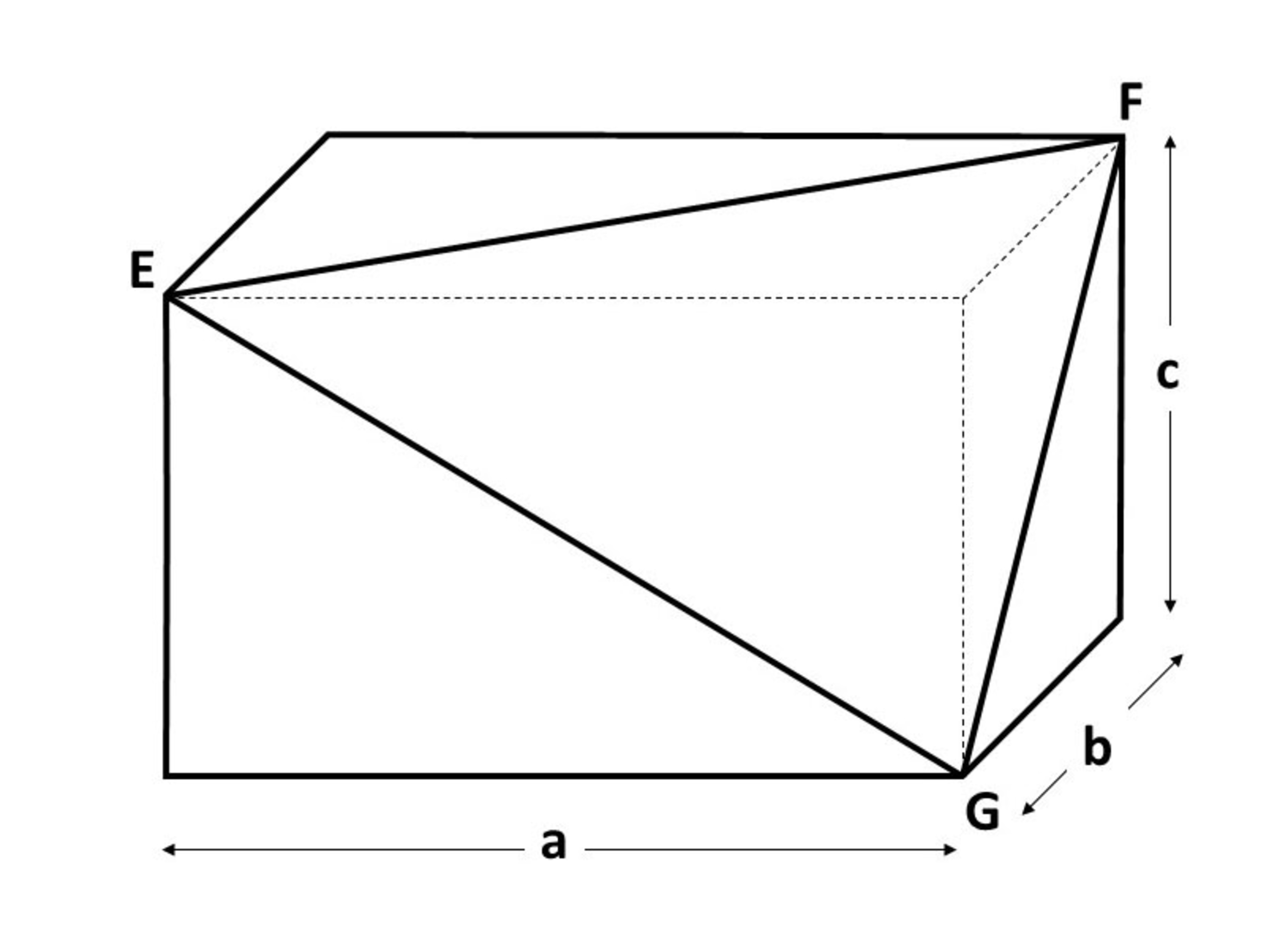
A rectangular cube (cuboid) is cut as shown, so that the cut goes through vertices E, F, and G. What is the area of the triangle EFG, if a=7, b=5, and c=4?
17.5
25.76
24.54
The area of a triangle cannot be found without knowing the height.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

The sides of the triangle are the diagonals of the faces of the cuboid.
They are from Pythagorean theorem 7 2 + 5 2 = 7 4 , 7 2 + 4 2 = 6 5 , 4 2 + 5 2 = 4 1
Heron's formula will give us the area of the triangle based on its sides.
The semi-perimeter s is the sum of the sides divided by two s ≈ 1 1 . 5 3 3
A = s ( s − 7 4 ) ( s − 6 5 ) ( s − 4 1 ) = 2 4 . 5 4