an obscure triangle
What is the smallest integer triangle in which the orthocenter lies on its nine-point circle? Submit the sum of the sides.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
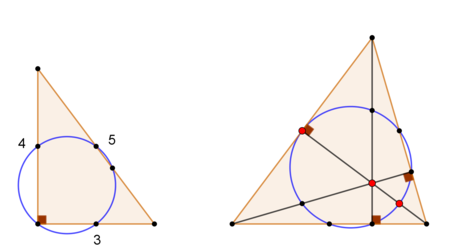 The nine-point circle passes through the foot of each altitude and through the midpoint of the line segment from each vertex of the triangle to the orthocentre, thus, in order for the circle to pass through the orthocentre as well, one of these segments must be of zero length. Otherwise, on every altitude, these three points would be collinear and the nine-point circle couldn’t pass through them. This means that the orthocentre will coincide with one vertex of the triangle, i.e. the triangle has to be a right-angled triangle. The smallest integer right triangle is the
3
-
4
-
5
triangle, thus the answer is
3
+
4
+
5
=
1
2
.
The nine-point circle passes through the foot of each altitude and through the midpoint of the line segment from each vertex of the triangle to the orthocentre, thus, in order for the circle to pass through the orthocentre as well, one of these segments must be of zero length. Otherwise, on every altitude, these three points would be collinear and the nine-point circle couldn’t pass through them. This means that the orthocentre will coincide with one vertex of the triangle, i.e. the triangle has to be a right-angled triangle. The smallest integer right triangle is the
3
-
4
-
5
triangle, thus the answer is
3
+
4
+
5
=
1
2
.
Recall that the nine point centre N is the midpoint of O H , where O is the circumcentre and H is the orthocentre; also the radius of the nine point circle is 2 1 R , where R is the circumradius.
Then H will lie on the nine point circle precisely when N H = 2 1 R , namely when O H = R , so that H lies on the circumcircle. But O H 2 = R 2 ( 1 − 8 cos A cos B cos C ) and hence we deduce that cos A cos B cos C = 0 , so that the triangle is right-angled. The smallest integer-sided right-angled triangle has sides 3 , 4 , 5 , making the answer 1 2 .
Here is a proof of the formula for O H . Note that sin 2 A + sin 2 B + sin 2 C = sin 2 A + sin 2 B + ( sin A cos B + cos A sin B ) 2 = sin 2 A + sin 2 B + ( 1 − cos 2 A ) cos 2 B + cos 2 A ( 1 − cos 2 B ) + 2 sin A cos A sin B cos B = 2 − 2 cos 2 A cos 2 B + 2 sin A cos A sin B cos B = 2 − 2 cos A cos B ( cos A cos B − sin A sin B ) = 2 + 2 cos A cos B cos C If we set up our origin at the circumcentre O , and let A , B , C have position vectors a , b , c , then H has position vector a + b + c , and hence O H 2 = ∣ ∣ a + b + c ∣ ∣ 2 = 3 R 2 + 2 ( a ⋅ b + a ⋅ c + b ⋅ c ) = R 2 ( 3 + 2 cos 2 A + 2 cos 2 B + 2 cos 2 C ) = R 2 ( 4 ( cos 2 A + cos 2 B + cos 2 C ) − 3 ) = R 2 ( 9 − 4 ( sin 2 A + sin 2 B + sin 2 C ) ) = R 2 ( 1 − 8 cos A cos B cos C )
Creative solution, but it isn't obvious to me where the O H 2 expression came from. Thanks.