An Odd-Only Generalization
Assume that A 1 A n + 1 , A 2 A n + 2 , A 3 A n + 3 , … … … and A n A 2 n are n ≥ 3 concurrent lines, where n is an odd positive integer. The point of concurrence is C .
A counter-clockwise rotating ray with its endpoint fixed at C and initial position along C A 1 passes, in its first full rotation, A i before A j whenever i < j .
Draw the segments A 1 A 2 , A 3 A 4 , A 5 A 6 … … … and A 2 n − 1 A 2 n .
Now we define the following function F .
F ( n ) = ( ∠ C A 1 A 2 + ∠ C A 2 A 1 ) + ( ∠ C A 3 A 4 + ∠ C A 4 A 3 ) + ( ∠ C A 5 A 6 + ∠ C A 6 A 5 ) + … … … + ( ∠ C A 2 n − 1 A 2 n + ∠ C A 2 n A 2 n − 1 ) .
The following figure illustrates the case for n = 3 with the defining angles for F ( 3 ) indicated.
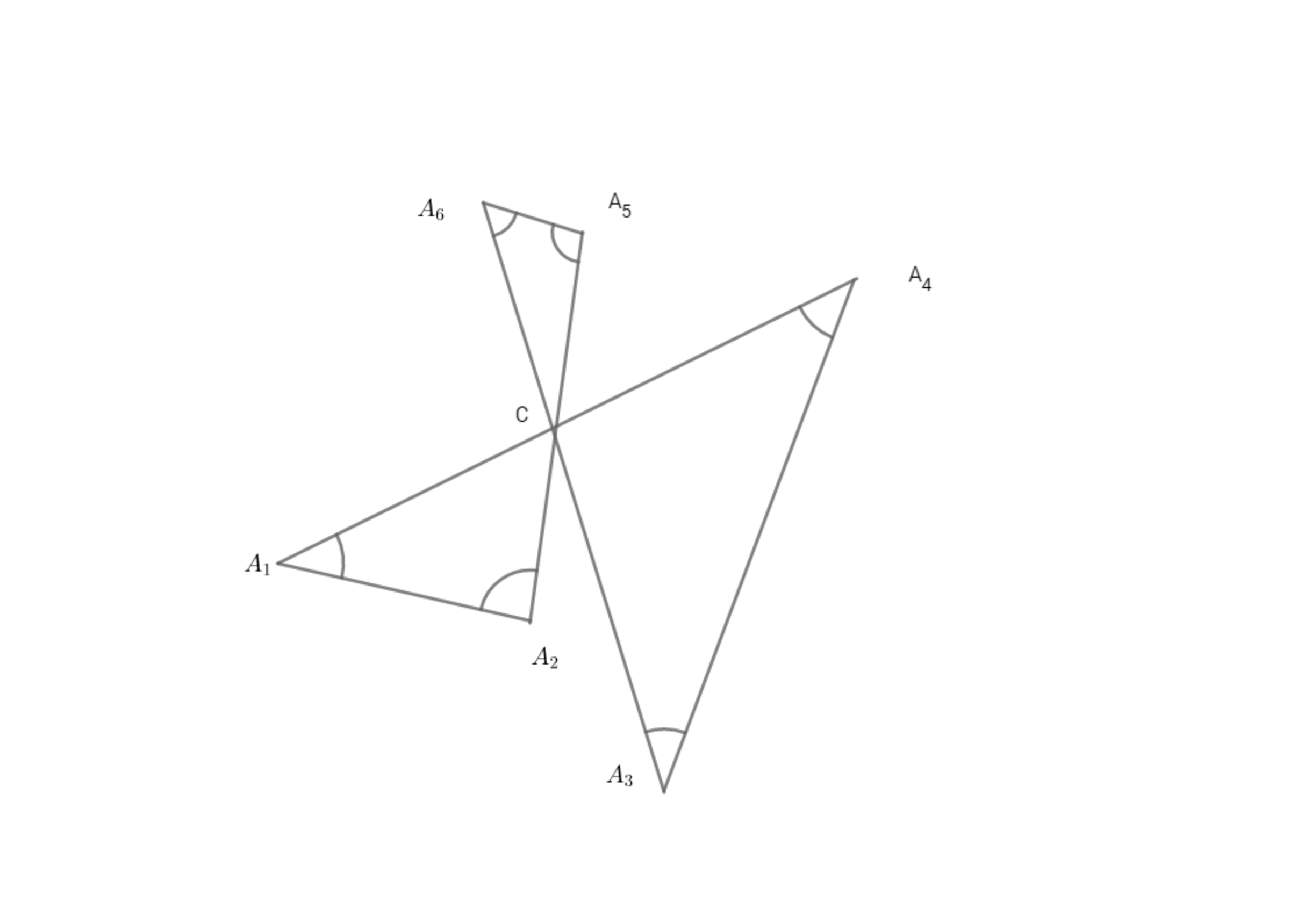
Find F ( 2 0 1 7 ) , in degrees.
The answer is 362880.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First notice, ∠ C A i A j contributes to F if and only if i − j = ± 1 and the minimum of i and j is an odd integer.
Now, we have, in degree measure, ∠ A 1 C A n + 1 = 1 8 0
[As A 1 , C , A n + 1 are collinear]
⟹ ∠ A 1 C A 2 + ∠ A 2 C A 3 + ∠ A 3 C A 4 + ∠ A 4 C A 5 + … … … + ∠ A n C A n + 1 = 1 8 0
⟹ ∠ A 1 C A 2 + ∠ A 2 + n C A 3 + n + ∠ A 3 C A 4 + ∠ A 4 + n C A 5 + n + … … … + ∠ A n C A n + 1 = 1 8 0
[As ∠ A i C A j and ∠ A i + n C A j + n are vertically opposite angles when i = j − 1 and j ≤ n ]
⟹ 1 8 0 − ( ∠ A 1 + ∠ A 2 ) + 1 8 0 − ( ∠ A 2 + n + ∠ A 3 + n ) + 1 8 0 − ( ∠ A 3 + ∠ A 4 ) + 1 8 0 − ( ∠ A 4 + n + A 5 + n ) + … … … + 1 8 0 − ( ∠ A n + A n + 1 ) = 1 8 0
⟹ n × 1 8 0 − ( ∠ A 1 + ∠ A 2 + ∠ A 2 + n + ∠ A 3 + n + ∠ A 3 + ∠ A 4 + ∠ A 4 + n + A 5 + n + … … … + ∠ A n + A n + 1 ) = 1 8 0
⟹ 1 8 0 n − F ( n ) = 1 8 0 [As, when i = j , A i + n and A j + n are different points]
⟹ F ( n ) = 1 8 0 ( n − 1 ) .