An old problem.
If 3 x 4 + 2 x 5 = 1 8 1 and x 1 , x 2 , x 3 , x 4 , and x 5 satisfy the system of equations below.
2 x 1 + x 2 + x 3 + x 4 + x 5 = m
x 1 + 2 x 2 + x 3 + x 4 + x 5 = 2 m
x 1 + x 2 + 2 x 3 + x 4 + x 5 = 4 m
x 1 + x 2 + x 3 + 2 x 4 + x 5 = 8 m
x 1 + x 2 + x 3 + x 4 + 2 x 5 = 1 6 m
find m
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Yep! That easy and rated a whooping 190 points!
Log in to reply
I am also surprised about its rating.
Its so simple !!!!!!!!!The equation is clearly symmetrical along the left leading diagonal, using gaussian elimination would be too long. Adding eq 1---> eq5 we see 6x1 + 6x2 + 6x3 + 6x4 + 6x5 = 31m hence sum of x s = 31/6m from equation 4 we see x4 + 31/6 = 8m this implies x4 = 8m - 31/6m , similarly x5 = 16 m - 31/6m. Subbing these values into the above equation ( 3x4 + 2x5 = 181) yields 24m - 31/2m + 32m - 31/3m = 181 . This will give m = 6
Write a solution
We can arrange the whole systems as matrix A times matrix X, and we can evaluate the values of all x’s with the inverse matrix A:
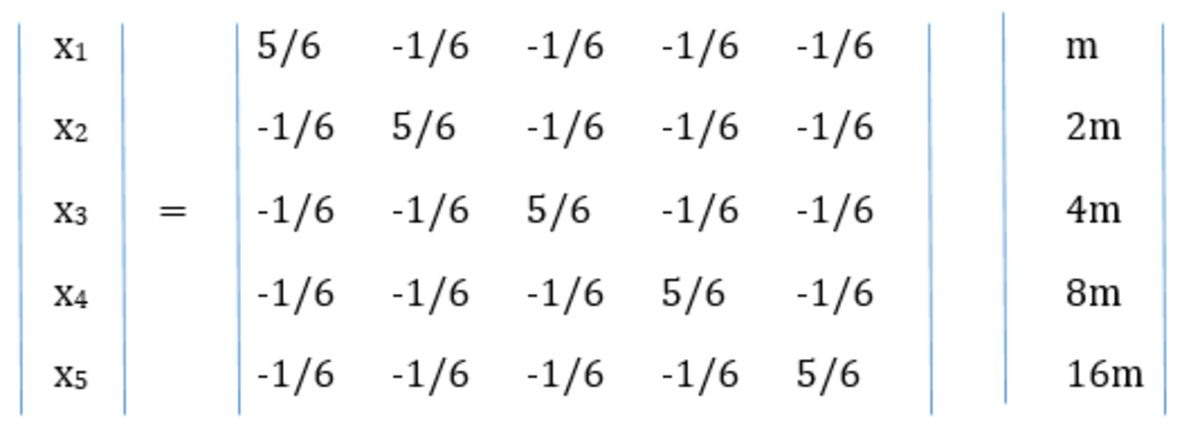
Then we can calculate:
x4 = (-1/6)(m+2m+4m+16m)+(5/6)(8m) = (17/6)m
x5 = (-1/6)(m+2m+4m+8m)+(5/6)(16m) = (65/6)m
3x4+2x5 = 181
(17/2)m+(65/3)m = 181
(181/6)m = 181
So m=6.
Adding all 5 equations of the system, we obtain:
6 ( x 1 + x 2 + x 3 + x 4 + x 5 ) = 3 1 m ⇒ x 1 + x 2 + x 3 + x 4 + x 5 = 6 3 1 m
giving us
1 8 1 = 3 x 4 + 2 x 5 = 3 ( 8 m − 6 3 1 m ) + 2 ( 1 6 m − 6 3 1 m ) = 6 1 8 1 m
hence m = 6 .