An Olympiad Problem!
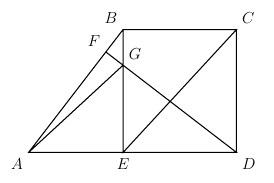 Trapezoid
A
B
C
D
has right angles at
C
and
D
, and
A
D
>
B
C
. Let
E
and
F
be the points on
A
D
and
A
B
, respectively, such that
∠
B
E
D
and
∠
D
F
A
are right angles. Let
G
be the point of intersection of segments
B
E
and
D
F
. If
∠
C
E
D
=
5
8
∘
and
∠
F
D
E
=
4
1
∘
, what is
m
∠
G
A
B
?
Trapezoid
A
B
C
D
has right angles at
C
and
D
, and
A
D
>
B
C
. Let
E
and
F
be the points on
A
D
and
A
B
, respectively, such that
∠
B
E
D
and
∠
D
F
A
are right angles. Let
G
be the point of intersection of segments
B
E
and
D
F
. If
∠
C
E
D
=
5
8
∘
and
∠
F
D
E
=
4
1
∘
, what is
m
∠
G
A
B
?
Disclaimer: This was an olympiad problem. All credits to the one who originally made this problem.
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
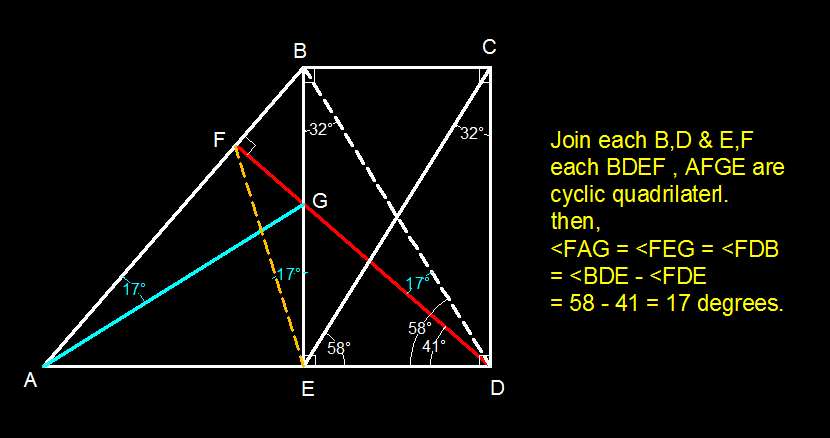
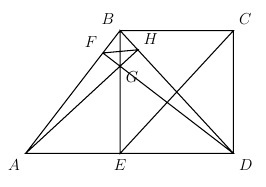 We start off by drawing
B
D
. Then we extend
A
G
to a point
H
on
B
D
. Since
D
F
and
B
E
are both altitudes of
△
A
B
D
, then
G
is the orthocenter. Similarly, we conclude that
A
H
⊥
B
D
. That means
A
F
H
D
is a cyclic quadrilateral and
m
∠
G
A
B
=
m
∠
F
D
B
=
5
8
−
4
1
=
1
7
.
We start off by drawing
B
D
. Then we extend
A
G
to a point
H
on
B
D
. Since
D
F
and
B
E
are both altitudes of
△
A
B
D
, then
G
is the orthocenter. Similarly, we conclude that
A
H
⊥
B
D
. That means
A
F
H
D
is a cyclic quadrilateral and
m
∠
G
A
B
=
m
∠
F
D
B
=
5
8
−
4
1
=
1
7
.
Same problem has appeared a few months back.
How have you concluded AFHD is cyclic ?? Please explain.
Log in to reply
From the fact that ∠ D F A = ∠ A H D = 9 0 ∘ , you can immediately conclude that by Thales' theorem , A F H D is cyclic.
Basically, I did the same way. But I think it should be shown how quadrilaterals are cyclic, specially BDEF.
Log in to reply
One of necessary and sufficient condition for a convex quadrilateral to be cyclic is that
an angle between a side and a diagonal is equal to the angle between the opposite side and the other diagonal.
That is, for covex quadrilateral BDEF :
angle between side DE and diagonal EB = <DEB = 90 degrees.
angle between opposite side BF and the another diagonal FD = <BFD = 90 degrees.
sinse, the two angles are equal which satisfy that codition, then the quadrilateral BDEF is cyclic.
Log in to reply
Thank you. I did not know this. So it was a long way I did.