An Oversimplified Image Application

Electricity and Magnetism Level pending

This link outlines a "method of images" solution for a grounded sphere with a charge outside. Essentially, we solve for the location and charge value of a virtual particle, such that the electric potential is zero at two points on opposite ends of the sphere. Conveniently, this solution results in zero potential everywhere on the sphere surface, as it must in the electrostatic case.

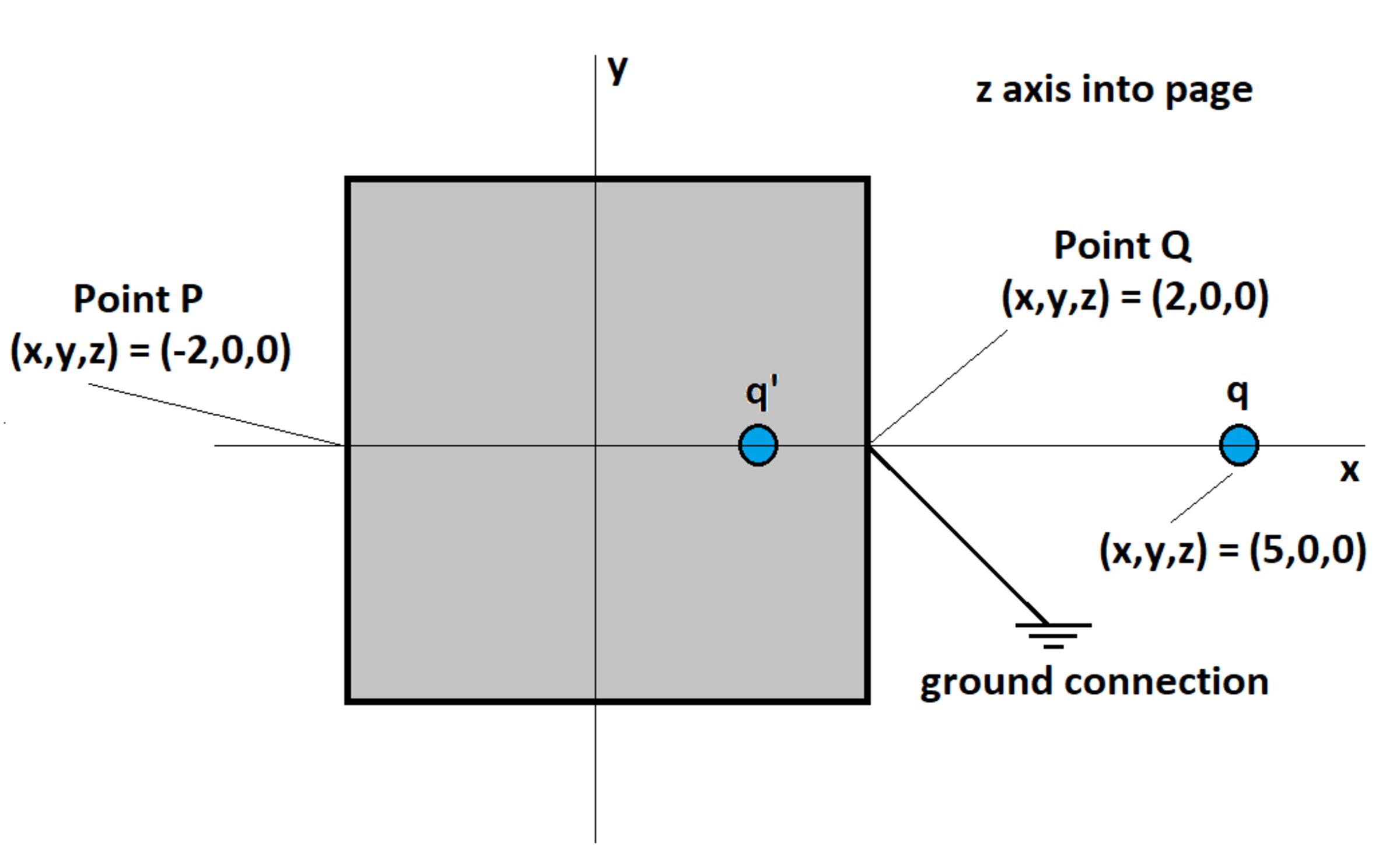
Suppose we try the same thing with a hollow conducting grounded cube of side length $4$ , centered on the origin. A charge $q$ is placed outside the cube, and we solve for an image charge $q'$ somewhere on the $x$ axis inside the cube which makes the electric potential zero at points $P$ and $Q$ . This solution yields zero potential at the centers of all faces, but does not result in zero potential everywhere on the cube surface. It is thus not a proper electrostatic solution.

In this scenario, what is the magnitude of the calculated electric potential at the point $(x,y,z) = (2,2,2)$ ?

Bonus: What might the actual charge distribution be? I have a guess, but I haven't checked it yet

Details and Assumptions:
1) $q = +1$
2) $\frac{1}{4 \pi \epsilon_0} = 1$

The answer is 0.1123.

1 solution

A Former Brilliant Member
Feb 7, 2020

Let the coordinates of $q'$ be $(x, 0,0)$ . Then $\dfrac{q}{3}+\dfrac{q'}{2-x}=0$ and $\dfrac{q}{7}+\dfrac{q'}{2+x}=0$ . Therefore $x=0.8, q'=-0.4q$ . Distance of $q$ from $(2,2,2)$ is $\sqrt {17}$ and that of $q'$ from $(2,2,2)$ is $\sqrt {9.44}$ . Therefore the potential at point $(2,2,2)$ is $\dfrac{q}{\sqrt {17}}-\dfrac{0.4q}{\sqrt {9.44}}=\boxed {0.1123467140555}$

An Oversimplified Image Application

The answer is 0.1123.

1 solution

0 pending reports