An unknown pitcher
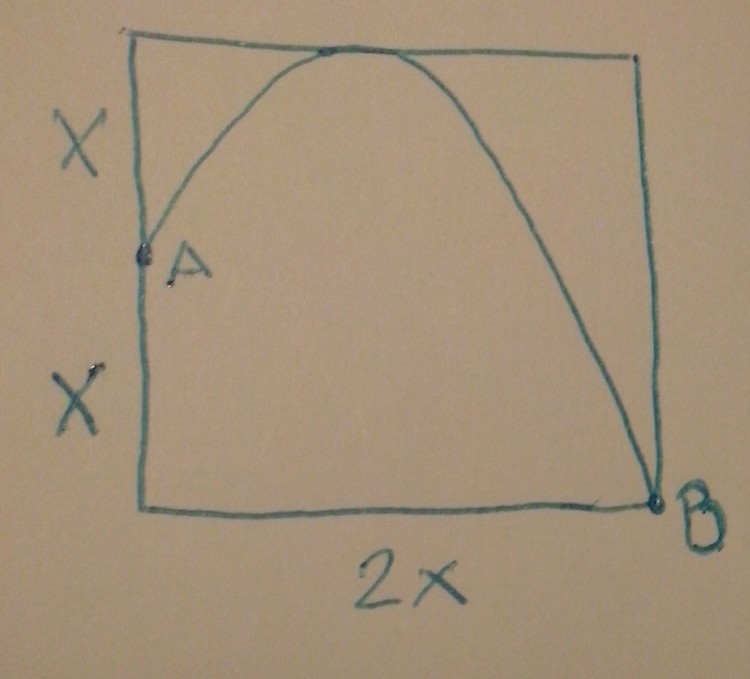 An unknown pitcher, with unknown weight, height, and age throws a ball of unknown weight and size, in a cubic room with unknown dimensions. He throws the ball at A, and the ball touches the roof and falls at B. At what angle (in degrees) did he throw the ball?
An unknown pitcher, with unknown weight, height, and age throws a ball of unknown weight and size, in a cubic room with unknown dimensions. He throws the ball at A, and the ball touches the roof and falls at B. At what angle (in degrees) did he throw the ball?
The answer is 67.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the initial velocity and the angle of throw with the horizon be v and θ respectively.
If the ball touches the ceiling at time t = t 1 , then:
0 = v sin θ − g t 1 ⇒ v sin θ = g t 1
Now, the vertical displacement y ( t ) at time t is given by:
y ( t ) = v sin θ t − 2 1 g t 2 = v sin θ ( t − 2 t 1 t 2 )
⇒ y ( t 1 ) = x = v sin θ ( t 1 − 2 t 1 t 1 2 ) = 2 1 v sin θ t 1
Let the ball hit point B at t 2 , then:
⇒ y ( t 2 ) = − x = v sin θ ( t 2 − 2 t 1 t 2 2 ) and since x = 2 1 v sin θ t 1 .
⇒ v sin θ ( t 2 − 2 t 1 t 2 2 ) = − 2 1 v sin θ t 1 ⇒ v sin θ ( t 2 − 2 t 1 t 2 2 + 2 t 1 ) = 0
⇒ t 2 − 2 t 1 t 2 2 + 2 t 1 = 0 ⇒ t 2 2 − 2 t 1 t 2 − t 1 2 = 0
⇒ t 2 = 2 2 t 1 + 4 t 1 2 + 4 t 1 2 = t 1 ( 1 + 2 )
We know that: v cos θ t 2 = 2 x ⇒ x = 2 1 v cos θ t 1 ( 1 + 2 ) .
⇒ x = 2 1 v sin θ t 1 = 2 1 v cos θ t 1 ( 1 + 2 ) ⇒ tan θ = 1 + 2
⇒ θ = tan − 1 1 + 2 = 6 7 . 5 ∘
Let me give every one a better graphic.
X -axis
V 0 cos θ t = 2 x
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Y -axis
0 = V 0 − g t 1
V 0 = g t 1
0 2 = ( g t 1 ) 2 − 2 g ( x )
( g t ) 2 = 2 g ( x )
g t 1 2 = 2 x
t 1 = g 2 x (time: he throws-touch the roof)
V f 2 = − 2 g ( − 2 x ) (since the roof until floor)
V f = 0 − g t 2
4 x g = g 2 t 2 2
t 2 = g 4 x
Total time
t t = g 4 x + g 2 x
V 0 sin θ = g t 1
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
V 0 cos θ t t V 0 sin θ = 2 x g t 1
V 0 cos θ V 0 sin θ = 2 x g t 1 t t
V 0 c o s θ V 0 s i n θ = 1 + 2
tan θ = 1 + 2
θ = 6 7 . 5 °