An unrelated triangle

Let the radius of the circle be $r$ . Since $\triangle ABD$ and $\triangle ADP$ are sharing the altitude $AE$ , this means that the areas of the two triangles are directly proportional to the base lengths that is:

$\begin{aligned} \frac {BD}{DP} & = \frac {[ABD]}{[ADP]} & \small \color{#3D99F6} \text{Since } 3[ABD] = 2[ADP] \\ & = \frac 23 \\ \implies BD & = \frac 23 DP & \small \color{#3D99F6} \text{Note that } BD+DP = r \\ BD+DP & = r \\ \frac 53 DP & = r \\ \implies DP & = \frac 35 r \end{aligned}$

By cosine rule , we have:

$\begin{aligned} DP^2 + AP^2 - 2(DP)(AP)\cos \alpha & = AD^2 \\ \left(\frac 35 r\right)^2 + r^2 - 2 \times \frac 35 r \times r \times \cos 120^\circ & = 7^2 \\ \frac {49}{25}r^2 & = 49 \\ \implies r & = 5 \end{aligned}$

Let $\angle ACP = \angle DAP = \beta$ and $\angle ADP = \gamma$ . By sine rule :

$\begin{aligned} \frac {\sin \angle DAP}{DP} & = \frac {\sin \angle ADP}{AP} = \frac {\sin \angle APD}{AD} \\ \frac {\sin \beta}3 & = \frac {\sin \gamma}5 = \frac {\sin \alpha}7 = \frac {\sqrt 3}{14} \end{aligned}$

$\implies \begin{cases} \sin \beta = \dfrac {3\sqrt 3}{14} & \implies \cos \beta = \dfrac {13}{14} \\ \sin \gamma = \dfrac {5\sqrt 3}{14} & \implies \cos \gamma = \dfrac {11}{14} \end{cases}$

Let $PF$ be the altitude of $\triangle PAC$ , then we have:

$\begin{aligned} [CPD] & = [CPF] - [DPF] \\ & = \frac 12 (CF)(PF) - \frac 12 (DF)(PF) \\ & = \frac 12 CP^2\sin \beta \cos \beta - \frac 12 DP^2 \sin \gamma \cos \gamma \\ & = \frac {5^2}2 \times \frac {3\sqrt 3}{14} \times \frac {13}{14} - \frac {3^2}2 \times \frac {5\sqrt 3}{14} \times \frac {11}{14} \\ & = \frac {60\sqrt 3}{49} \end{aligned}$

$\implies a+b+c = \boxed{112}$

The given ratio of areas implies that $PD=\frac{3}{5}AP$ as BP=AP. Using cosine formula on $\alpha=120^\circ$ of $\Delta APD$ $AP^2+(\frac{3}{5})^2AP^2+\frac{3}{5}AP^2=7^2\rightarrow AP=5$ . Hence PD=3, and CP=AP=5. Now the three sides of $\Delta BAD$ are AD=7, $AB=5\sqrt{3}$ and BD=2, we get $cos\angle BAD=\frac{4\sqrt3}{7}$ using cosine formula. Using the fact that angle at the center $\angle CPB$ is twice of the angle at the circumference $\angle BAD$ , we get $cos\angle CPD=cos\angle CPB=2cos^2\angle BAD -1=\frac{47}{49}$ giving $sin\angle CPD= \frac{8\sqrt{3}}{49}$ . Now knowing the sides and sine of the included angle area is $\frac{1}{2} \cdot 3 \cdot 5 \cdot \frac {8\sqrt{3}}{49} = \frac{60\sqrt{3}}{49}$ thus the answer is 112.

We can easily prove that since $AD$ divides $\Delta ABP$ into two triangles at a $3:2$ ratio, then $AD$ also divides $BP$ by such proportion. That is, $\frac {\Delta ADP}{\Delta ADB} = \frac{DP}{DB} = \frac{3}{2}$ . (See note below)

Let $x$ be one fifth of the length of $PB$ , so that $DB = 2x$ and $DP = 3x$ . From here we can express the areas of both triangles in terms of $x$ .

By Heron's formula, we get the area of $\Delta ADP$ as:

$\Delta ADP = \frac{1}{4} \sqrt{ -(256x^4 - 3332x^2 + 2401)}$

In a similar way,

$\Delta ADB = \frac{1}{4} \sqrt{ -(5041x^4 - 7742x^2 + 2401)}$

Equating these values to the ratio, and simplifying the equation, we get

$44345x^4 - 56350x^2 + 12005 = 0$

$(x^2 - 1)(44345x^2 - 12005) = 0$

$x = \pm 1 \:\:\: ; x = \pm \frac{7}{\sqrt{181}}$

Clearly, there are two positive values of $x$ . However, only the value $x=1$ conforms to the triangle inequality when substituted.

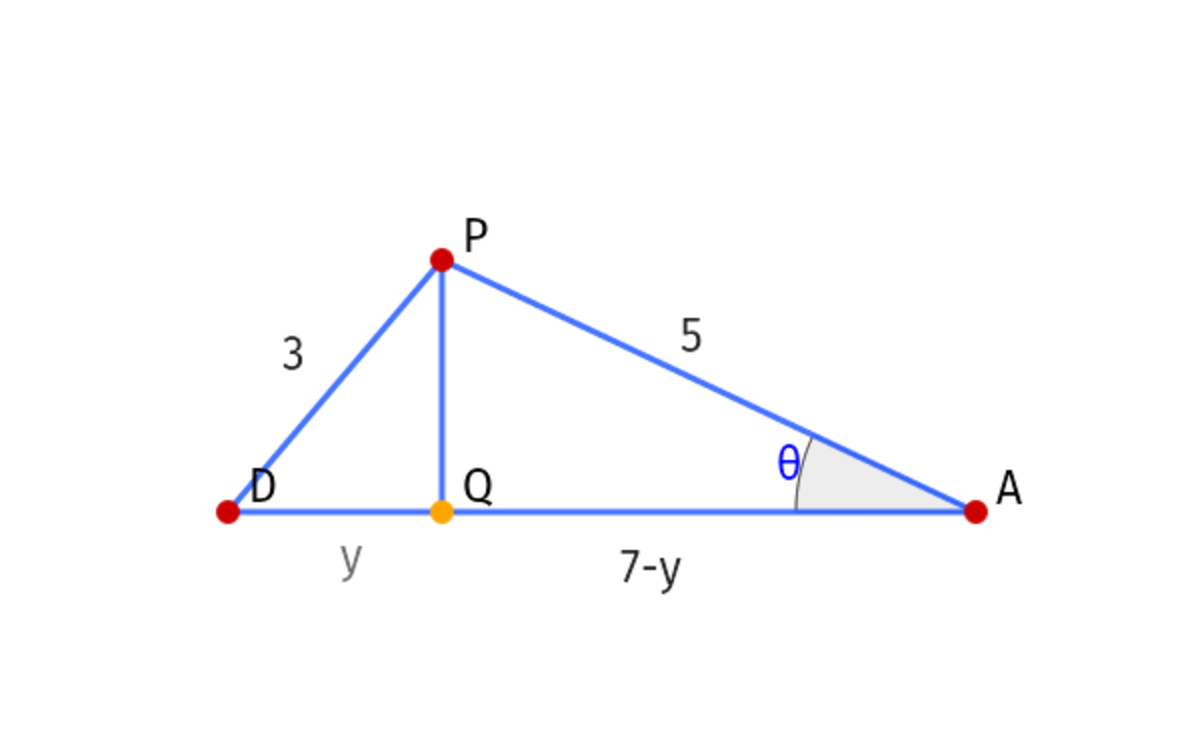
Now, substituting that, we get the dimensions for $\Delta ADP$ . We now draw an altitude from vertex $P$ to $AD$ at a point we'll name $Q$ . From there, we can determine lengths $DQ$ and $AQ$ , using this.

$9 - y^2 = 25 - (7-y)^2$

Solving that gives $y = \frac{33}{14}$ and $7 - y = \frac{65}{14}$ .

Now, we can find $\theta$ . I mean, $\cos \theta$ .

$\cos \theta = \frac{13}{14}$

From which we can derive

$\sin \theta = \frac{3 \sqrt{3}}{14}$

$\sin 2\theta = \frac{39 \sqrt{3}}{98}$

$\cos 2\theta = \frac{71}{98}$

Now, going back to the circle. Observe that $\angle PAC \cong \angle PCA$ , so $\angle PCA = \theta$ . It then follows that $\angle CPA = 180 - 2\theta$ . And $\angle CPD = 60 - 2 \theta$ .

Now, we are equipped with all the necessary requirements for the area of $\Delta CPD$ .

$\Delta CPD = \frac{1}{2} cd \sin P$

$= \frac{1}{2} \cdot 3 \cdot 5 \cdot \sin (60 - 2\theta)$

$= \frac{15}{2} ( \sin 60 \cos 2\theta - \cos 60 \sin 2\theta)$

$= \frac{15}{2} ( \frac{\sqrt{3}}{2} \cdot \frac{71}{98} - \frac{1}{2} \cdot \frac{39 \sqrt{3}}{98})$

$= \frac{15}{2} ( \frac{8 \sqrt{3}}{49} )$

$= \frac{60 \sqrt{3}}{49}$

So, $60 + 3 + 49 = \boxed {112}$ .

Note:

If we look at $PB$ as the base of $\Delta APB$ , we can see that as well as for both triangles $\Delta APD$ and $\Delta ABD$ , their heights are the same. So, their areas are directly proportional to the lengths of these bases, i.e., the lengths $PD$ and $BD$ .