An Unusual Equable Triangle
I'm thinking of a triangle where the area is numerically the same as the perimeter and in which the centroid , , and nine-point circle center, , both lie on the incircle, centered at . If is the length of the shortest side of the triangle, submit .
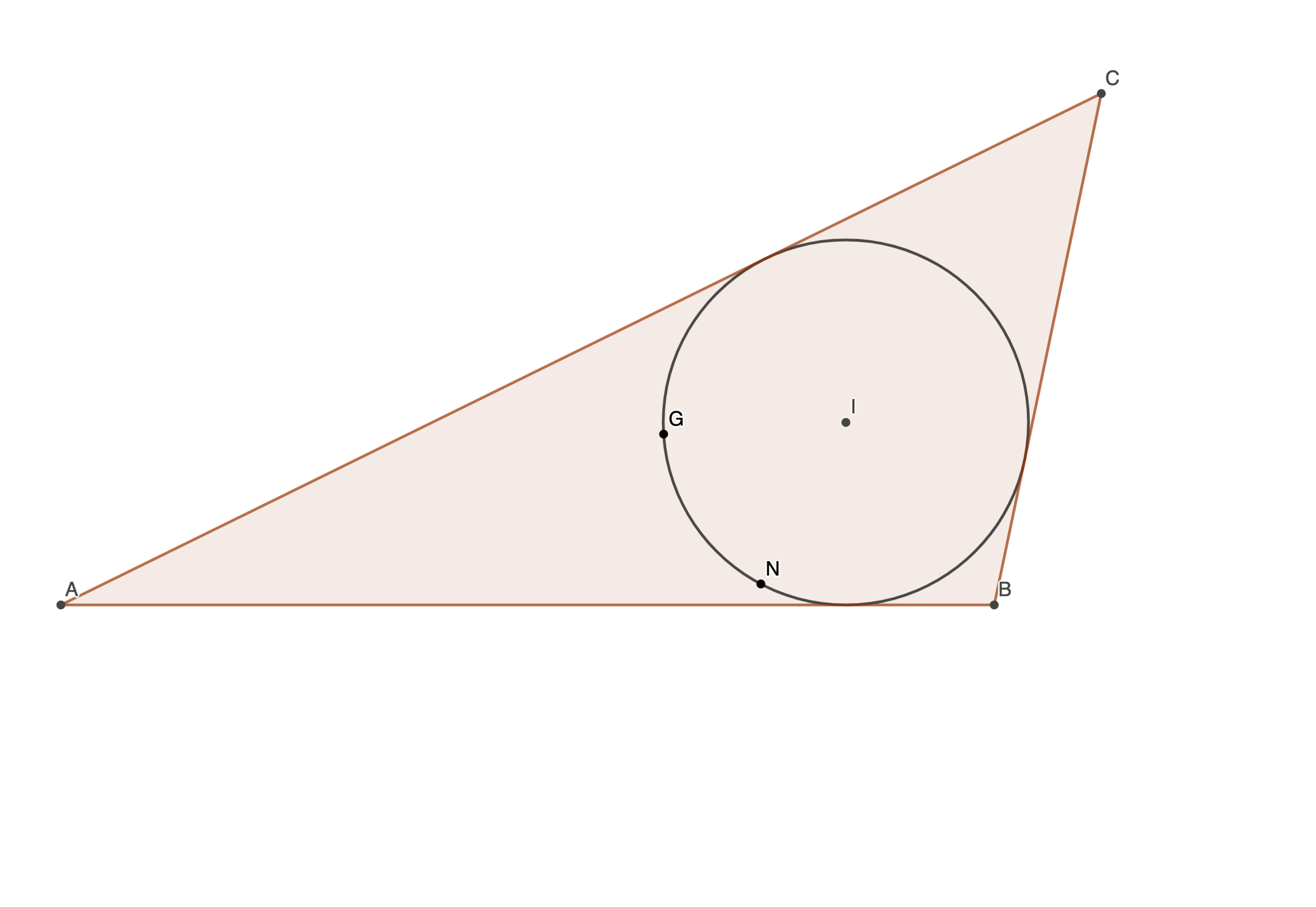
The answer is 576622.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
So we can use s for the triangle's semiperimeter, let's define the shortest side to be a (which matches the diagram in the question).
All equable triangles (indeed, all equable tangential polygons) have inradius 2 ; just equate the area r s and the perimeter 2 s .
Now it's time to look up formulas for the distances between centres. In any triangle, the distance between the incentre I and the centre of the nine-point circle N is I N = 2 R − 2 r
The distance between the incentre and the centroid G is I G = 3 1 5 r 2 − 1 6 R r + s 2
In this case, we want r = I G = I N = 2 ; solving the above we get R = 8 , s = 4 1 7
By definition of s , we have a + b + c = 8 1 7 . Now, using 2 R r = a + b + c a b c we get a b c = 2 5 6 1 7
Equating area formulas, r s r 2 s = s ( s − a ) ( s − b ) ( s − c ) = ( s − a ) ( s − b ) ( s − c ) = s 3 − ( a + b + c ) s 2 + ( b c + c a + a b ) s − a b c = − s 3 + ( b c + c a + a b ) s − a b c
Rearranging, this gives b c + c a + a b = s r 2 s + s 3 + a b c = 3 4 0
So the sidelengths a , b , c are the roots of the cubic x 3 − 8 1 7 x 2 + 3 4 0 x − 2 5 6 1 7 = 0
I don't think this factorises nicely; numerically, the smallest root is 5 . 7 6 6 2 2 … giving the answer 5 7 6 6 2 2 .