Analog of "Least Action" for Circuits?

Electricity and Magnetism Level 3

A 1-amp current source feeds a parallel set of resistors as shown below. Given that the two resistor currents must sum to equal the source current, how much current should flow in the $1 \, \Omega$ resistor in order for the total power dissipated in the resistors to be minimized?

Note: Analyze the problem with the specified requirement in mind, rather than using known rules. How does this relate to real life?

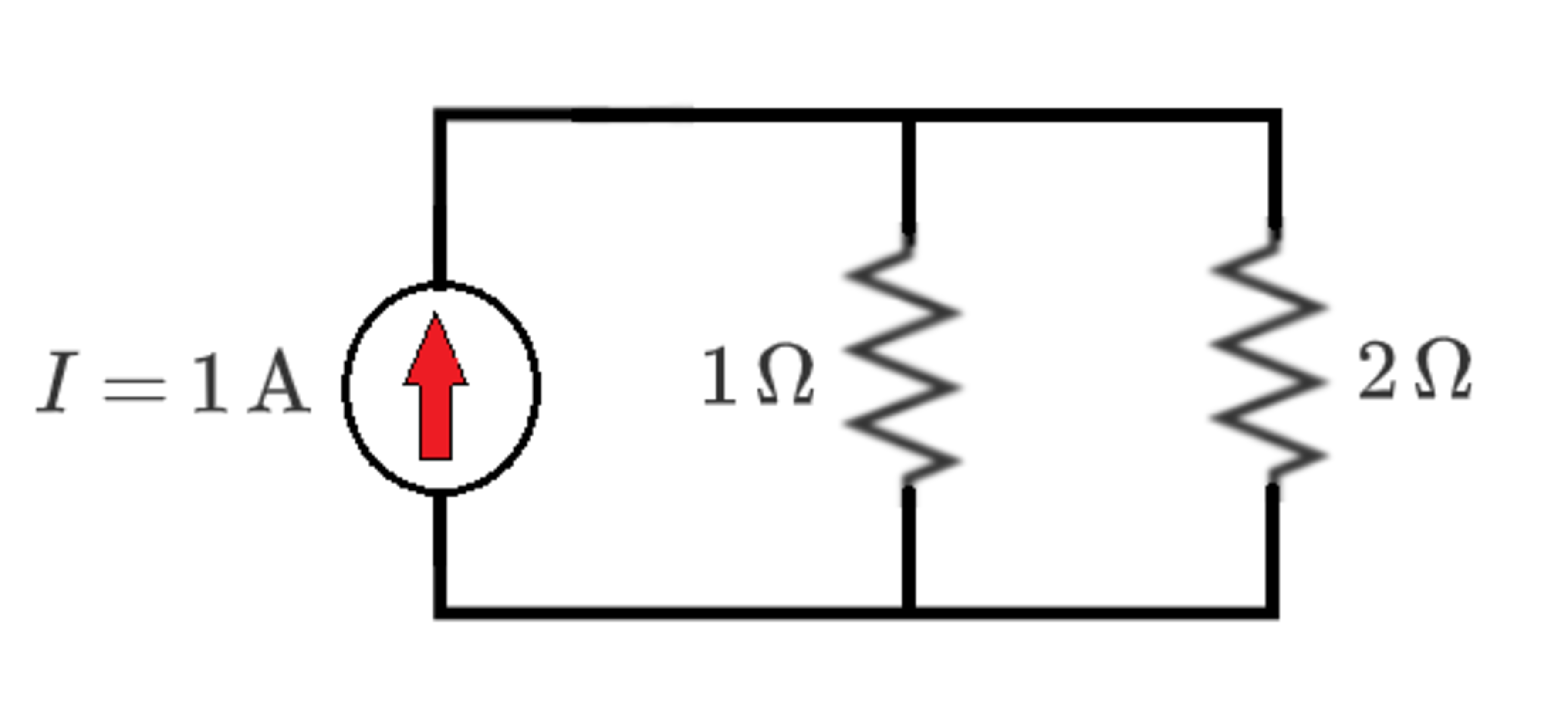
The answer is 0.66666.

1 solution

Parth Sankhe
Dec 1, 2018

Dissipative power = $i^2r$

$i^2(1)+(1-i)^2(2)$ should be minimum.

Making the derivative = 0,

$2i-2(1-i)(2)=0$ $\rightarrow$ $i=\frac {2}{3}$

It also makes sense to just find out what current would flow through each resistor irrespective of the power, since the parallel arrangement of resistors already accounts for the lowest power dissipation possible.

$R_2 = 2R_1$

Thus, $i_1=2i_2; i_1 + i_2 =1$

$i_1=0.667$

@Steven Chase How does this relate to life???

Aaghaz Mahajan - 2 years, 6 months ago

The "least power" principle turns out to be equivalent to the well-known current divider principle used in circuit analysis.

Steven Chase - 2 years, 6 months ago

Ohhh.........I didn't know that............Thanks :)

Aaghaz Mahajan - 2 years, 6 months ago

Analog of "Least Action" for Circuits?

The answer is 0.66666.

1 solution

0 pending reports