Analog Watch!

Geometry Level 1

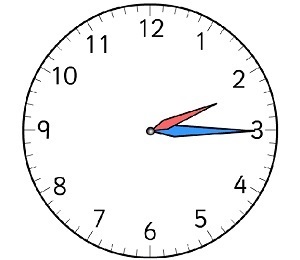What is the angle (in degrees) produced between the little hand (hours) and big hand (minutes) when the time is 2:15 PM?

22.5 30 20 7.5

10 solutions

Adam Phúc Nguyễn
Aug 31, 2015

In 15 minutes the minute hand went: $15\times \frac{360°}{60}=90°$ In 15 minutes the hour hand went: ( from 2 o'clock) $15\times \frac{30°}{60}=7.5°$ In 2 hours the hour hand went: $\frac{360°}{6}\times2=60°$ Therefore the angle produced is: $90°-7.5°-60°=\boxed{22.5°}$

Sorry but could please explain in a bit more detail

Temas Mukesh - 5 years, 9 months ago

60 minutes in an hour.
So when the hour hand has moved to the next hour, the minute hand would have completed one full rotation or 360 degrees.
60 minutes are equivalent to 360 degrees of rotation for the minute hand. Thus, one minute is equivalent to ( 360/60) : 6 degrees . Thus minute hand covers 6 degrees in a minute.
It takes 12 hours for the hour hand to cover 360 degrees (one full rotation). Thus in an hour, it completes: 360/12 = 30 degrees. -Notice however that say from 12'o clock to 1'o clock, the hour hand advances gradually and not abruptly. So in 15 minutes or 1/4 th of an hour, it would have already rotated by 30*(1/4) = 7.5 degrees............................(Ref 1)
Thus when it is exactly 2:00 pm, the hour hand points exactly at 2 and the minute hand points exactly at 12
In 10 minutes the minute hand will point at 2 and in 15 minutes, the minute hand will point at 3.
Thus for the minute hand to travel from 2 to 3, it takes 5 minutes equivalent to 5*6 degrees = 30 degrees.
Thus angle between 2 and 3 is 30 degrees..............................(Ref 2)
However by the time the minute hand reaches 3 after starting from 12, the hour hand is not pointing exactly at 2 any more. In those 15 minutes, It has advanced by 7.5 degrees from 2 as pointed out in Ref 1.
Thus minute hand has moved by 30 degrees from 2. (from Ref 2) and the hour hand has moved by 7.5 degrees from 2 (from statement above).
Thus difference in angle between both hands = 30 - 7.5 = 22.5 degrees.

Harimanjunathan Sankaranarayanan - 5 years, 9 months ago

You should explain the $30^{\circ}$ part for clarity.

MD Omur Faruque - 5 years, 9 months ago

But the question doesn't give u any information about the stsrting point which means it's just 30 degrees

Mateusz Franiczek - 2 years, 7 months ago

Mamun Abdullah
Aug 31, 2015

In the analog watch, create 360 degree in the center and analog watch is divided into 12 same arc(Hours).

So difference between one hours to next hours is = 360/12=30 degree. That's means, angle between hours 2 to 3 is 30 degree.

But, as Second hand is on the 15 minutes. So, hand of hour is slightly fall from 2.

As, Hours hand is move 30 degree when Minutes Hand is move 360 degree. So after move Minutes hand as 90 degree(12 to 3) then Hours hand will be move=(30x60)/360 = 7.5 degree. So the falling angle of Hours hand is 7.5 degree.

So. the Angle between Hours and Minutes hand is= 30-7.5 = 22.5 degree.

I'm not that good at math but... Isn't (30x60)/360= 1800/360=5 ??? I mean I haven't read what you wrote I just came and read the answer. I got the answer 24, I didn't do a lot of math, I just thought it was obvious.

A Former Brilliant Member - 3 years, 6 months ago

Arunima Mitra
Sep 23, 2015

In 1 hour, hour hand traverses 30 deg. , In 15 mins, hour hand will therefore traverse 30/4 =7.5 deg.

Angle between 2 and 3 of hour hand = 360/12= 30 deg .. Therefore answer=30 – 7.5= 22.5 degrees...

Hadia Qadir
Sep 2, 2015

2.5 degrees because it is not a full 30 degrees due to the constant motion of the smaller hand. The small hand should be 1/4 through between '2' and '3' at 2:15.

You assume it is the smallest angle that is required! If so solutions are correct, but whaty is it if the solution required is the larger. Reword the question correctly.

Keith Hodgson - 4 years, 10 months ago

I thought of it like this: 90 degrees = 15 min. 15/5=3. And like every 5 min is 30 degrees. But the little hand were pointing at one less. so 30/5 = 6. every 1 min = 6 degrees. The little hand was pointing at 4 mins which is 24 degrees... HELP ME PLS I NEED TO UNDERSTAND IT! And thank you.

A Former Brilliant Member - 3 years, 6 months ago

Sunil Pradhan
May 10, 2016

ø = 11/2 m – 30 h where ø = angle between 2 hands of a clock. h = hours completed. m = minutes completed.

here h = 2 hr, m = 15 minutes. substituting in the formula,

ø = 11/2 × 15 – 30 × 2

= 82.5 – 60 = 22.5

Sankar Subramoni
Sep 5, 2015

Angle between 2and 3 is 360/12=30.Hour needle has moved 1/4 th of an Hour it has moved by 7.5 degree.30-7.5 is 22.5 degree.

Tantri Wardani
Sep 2, 2015

30-(30 x 1/4) =(30 x 1) - ( 30 x 1/4 ) = 30 x ( 1-1/4 ) = 30 x 3/4 = 22,5

Akshay Patil
Sep 2, 2015

I hour= 30 degree 1 hour= 5 subdivision when minute hand moves by 15 minutes the hour hand moves by 1.25 subdivision So if 5 subdivision corresponds to 30 degrees (5-1.25) subdivision corresponds to how much degree? 3.75*30/5 =22.5

Achille 'Gilles'
Sep 2, 2015

A full rotation of the short hand is 12 hours and it is at 2:15 (or 2,25) of its course so: 2,25 / 12 * 360° = 67,5°

Long hand is at 90° so the difference is 90° - 67,5° = 22,5°

Nano Noor
Sep 1, 2015

we can use a simple rule : (number of hours *30) - (11/2 * number of minutes ) note that 1 o'clock = 13 hours , 2 o'clock = 14 hours .. So , by applying this rule we find that : (14 *30 ) - (11/2 * 15) = 420 - 82.5 = 337.5 (which is the big angle) the small angle : 360 - 337.5 = 22.5

Analog Watch!

10 solutions

0 pending reports