Analytic Geometry - Parabola 2
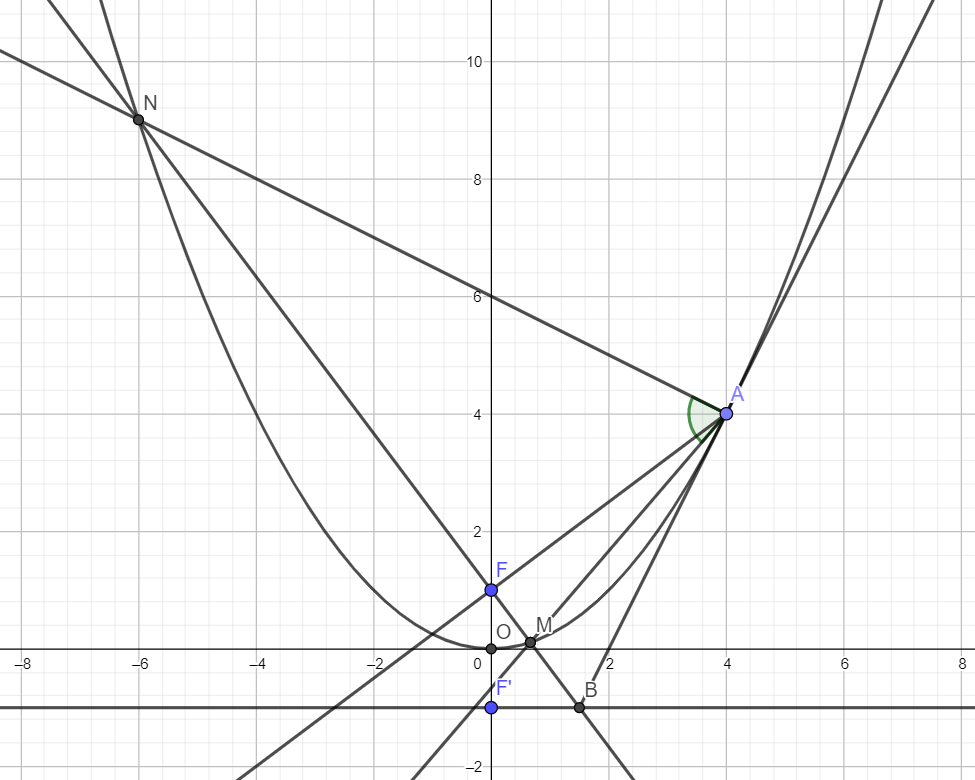 The focus of the parabola
is
, the directrix is
, let
be the arbitrary point
in the first quadrant
on the parabola.The line passing through
is perpendicular to
and intersects with the directrix at point
, the parabola at point
,
, respectively.
The focus of the parabola
is
, the directrix is
, let
be the arbitrary point
in the first quadrant
on the parabola.The line passing through
is perpendicular to
and intersects with the directrix at point
, the parabola at point
,
, respectively.
Question 1 : Is tangent to the parabola?
Question 2 : If , find the coordinate of point .
How to submit:
Let and be the answers to Question 1 and Question 2 .
If you think the statement in Question 1 is true, , otherwise .
For Question 2 , The coordinate of point is , . If you think there are more than one possible point, add up the corresponding together to get . Notice that is in the first quadrant .
Submit .
The answer is 5358.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A parabola in the form of x 2 = 4 y has a focus of F ( 0 , 1 ) and a directrix of y = − 1 .
Let the x -coordinate of A be p . Since A is on x 2 = 4 y , its coordinates are A ( p , 4 p 2 ) .
Line A F then has a slope of m A F = 4 p p 2 − 4 .
Since B F is perpendicular to A F , it has a slope of m B F = − p 2 − 4 4 p .
Since B F goes through F ( 0 , 1 ) , its equation is y = − p 2 − 4 4 p x + 1 .
Since B is on y = − 1 and y = − p 2 − 4 4 p x + 1 , its coordinates are B ( 2 p p 2 − 4 , − 1 ) .
Line A B then has a slope of m A B = 2 p .
The tangent line to x 2 = 4 y at x = p also has a slope of y ′ = 2 p . Therefore, A B is tangent to the parabola, so X = 1 .
Since M and N are on x 2 = 4 y and y = − p 2 − 4 4 p x + 1 , their coordinates are M ( p + 2 2 ( p − 2 ) , ( p + 2 ) 2 ( p − 2 ) 2 ) and N ( p − 2 − 2 ( p + 2 ) , ( p − 2 ) 2 ( p + 2 ) 2 ) .
Line A M then has a slope of m A M = 4 p + 8 p 2 + 4 p − 4 and line A N then has a slope of m A N = 4 p − 8 p 2 − 4 p − 4 .
For A M ⊥ A N , m A M ⋅ m A N = − 1 , or ( 4 p + 8 p 2 + 4 p − 4 ) ( 4 p − 8 p 2 − 4 p − 4 ) = − 1 . This simplifies to ( p 2 − 1 2 ) ( p 2 + 4 ) = 0 , whose only positive real solution (for the first quadrant) is p = 2 3 .
Therefore, the coordinates of A are A ( p , 4 p 2 ) = A ( 2 3 , 3 ) , which means Y = y − x = 3 − 2 3 .
Therefore, ⌊ 1 0 0 0 0 ( X + Y ) ⌋ = ⌊ 1 0 0 0 0 ( 1 + 3 − 2 3 ) ⌋ = 5 3 5 8 .