Analytical Geometry!
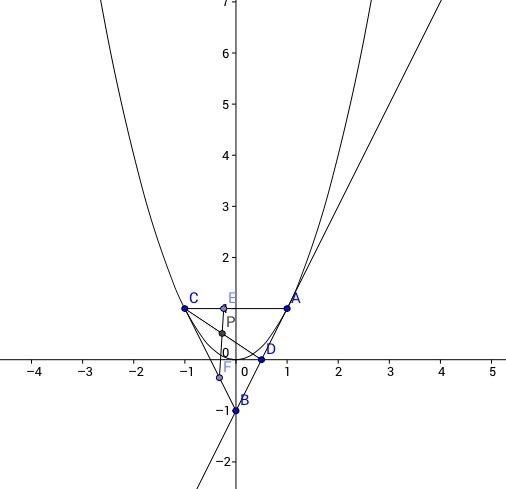
Draw a tangent line of parabola at the point . Suppose the line intersects the -axis and -axis at and respectively. Let point be on the parabola and point on such that . Let point be on such that and . Assume that intersects at point . When point moves along the parabola, the equation of the trail of can be expressed in the form . Where , find the value of .
- This problem is not original.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that the equation of the tangent line passing through ( 1 , 1 ) is y = 2 x − 1 . And D is the midpoint of A B .
Let γ = C P C D , t 1 = C E C A = 1 + λ 1 , t 2 = C F C B = 1 + λ 2 . Then t 1 + t 2 = 3 .
We know that A D = 2 A B , [ C A B ] = 2 [ C A D ] = 2 [ C B D ] . But we have t 1 t 2 1 = ( C A ) ( C B ) ( C E ) ( C F ) = [ C A B ] [ C E F ] = 2 [ C A D ] [ C E P ] + 2 [ C E D ] [ C F P ] = 2 t 1 t 2 γ 3 .
Thus, γ = 2 3 . And P is the centroid of △ A B C .
Then consider the points P ( x , y ) and C ( x 0 , x 0 2 ) . Since C is different from A , x 0 = 1 . And the coordinates of P are ( 3 1 + x 0 , 3 x 0 2 ) . Keeping in mind that x = 3 2 . Eliminating x 0 , we obtain y = 3 1 ( 3 x − 1 ) 2 . So the equation of the trail is y = 3 1 ( 3 x − 1 ) 2 , x = 3 2 .
Therefore, the answer is 3 − 1 + 3 = 5 .