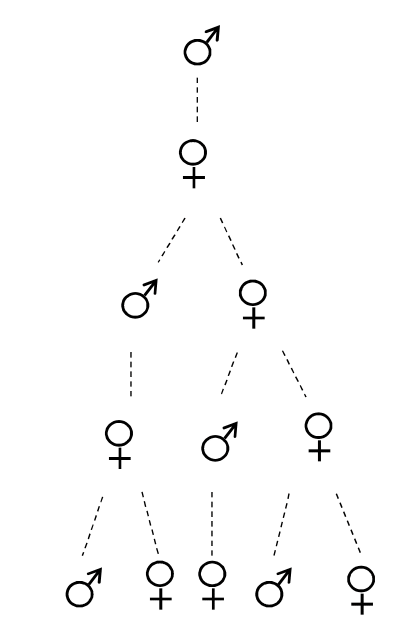
Ancestry of Bees

Probability Level 2

Sally knows the following about the reproduction of bees:

If a bee is male, it has just one parent who is female.
If a bee is female, it has two parents: one male and one female.

She observes that a male bee has 1 parent, 2 grandparents, and 3 great-grandparents.

How many great-great-grandparents does a male bee have?

Clarification: The reproduction of bees doesn't behave in the same way as that of humans. Fertilized eggs will hatch into female worker bees, while unfertilized eggs will become drones or honey bee males.

4 5 6 7

2 solutions

Marta Reece
Aug 8, 2017

Peter Macgregor
Aug 10, 2017

I initially solved the problem, like Marta, by drawing a family tree going back through the generations. The number of ancestors of a male bee increases according to the pattern 1,2,3,5,8,13.....

Hang on! They are breeding like rabbits! see this link .

Here is a brief proof that the series continues to produce the Fibonacci numbers.

Let $M(n)$ be the number of ancestors going back n generations from a single male bee. We have the initial conditions $M(0)=1$ and $M(1)=1$ . Similarly let F(n) be the number of ancestors going back n generations from a single female bee.

By looking at the structure of the tree (and thinking for a little bit) you can see that

$M(n)=F(n-1) \dots(1)$

$F(n)=M(n-1)+F(n-1) \dots(2)$

Now change the argument in (1) to get

$M(n+1)=F(n)$

Substitute into this from (2) to get

$M(n+1)=M(n-1)+F(n-1)$

Substitute into this from (1) to get

$M(n+1)=M(n-1)+M(n)$

This is indeed the Fibonacci recurrence relation. With our initial conditions $M(0)=1$ and $M(1)=1$ it reproduces the numbers 1,1,2,3,5,8,13,21....... and so on.

Ancestry of Bees

2 solutions

0 pending reports