Anchoring Angles

Probability Level 4

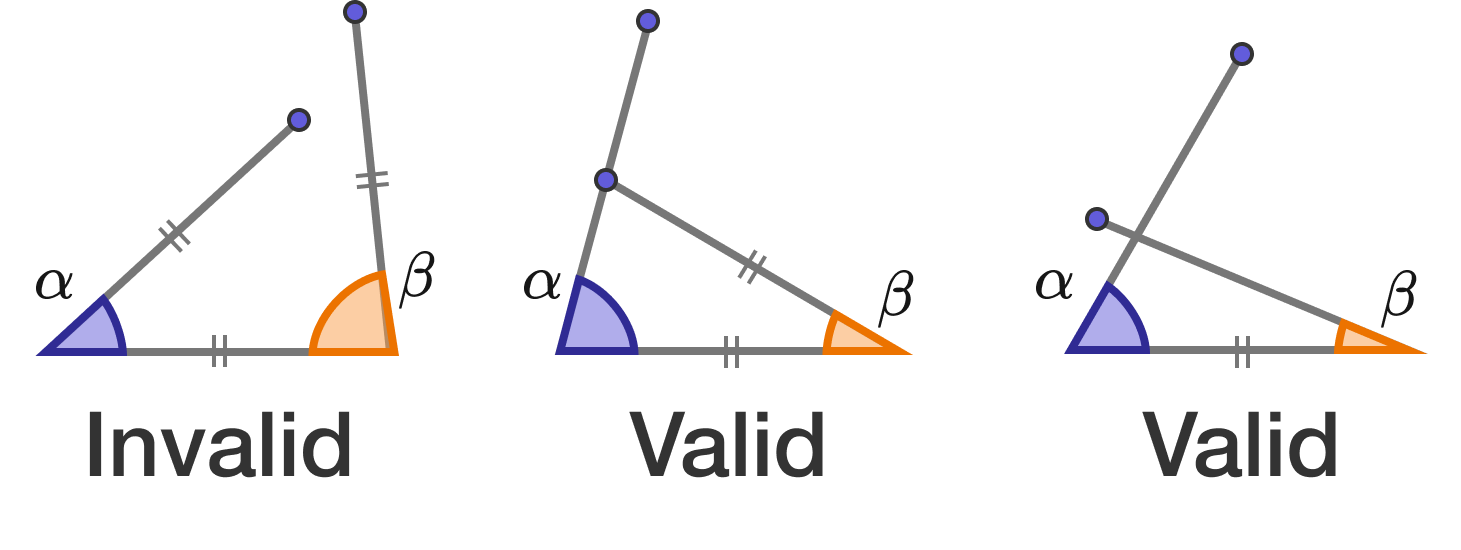
There are 3 congruent segments, 2 of which each have a blue point on one end.

Now, as shown in the diagram, the 3 segments are joined such that only the 2 blue ends can freely move at random, forming a triangle sometimes or failing to form one some other times, depending on the angles $\alpha$ and $\beta.$

What is the probability that two angles enclose a triangle, as illustrated by the latter two cases marked "valid"?

\frac{1}{36}

\frac{1}{18}

\frac{1}{12}

\frac{1}{9}

\frac{1}{6}

\frac{1}{4}

\frac{1}{3}

None of the above

1 solution

Otto Bretscher
Oct 18, 2018

By symmetry, we can assume that $\alpha\leq\pi$ . For $\alpha\leq\frac{\pi}{3}$ we want $\beta\leq\frac{\pi-\alpha}{2}$ and for $\frac{\pi}{3}\leq\alpha\leq\frac{\pi}{2}$ we want $\beta\leq\pi-2\alpha$ , as illustrated in the left "Valid" figure above. Thus the probability we seek is $\frac{\pi^2/6}{2\pi^2}=\boxed{\frac{1}{12}}$ .

Anchoring Angles

1 solution

0 pending reports