Ancient aliens

Classical Mechanics Level 3

NASA has captured an extraterrestrial space probe that has been in space for millions of years. The probe was operated by a kind of radionuclide battery, which on launch consisted of a pure block of plutonium-244. Now, the isotope ratio between thorium-232 and plutonium-244 is 1:1 due to the radioactive decay ( N Pu = N Th ) . (N_\text{Pu} = N_\text{Th}).

How long was the probe in space? (Specify the time in millions of years and round it to the nearest integer.)

Details and Assumptions:

  • Plutonium-244 decays in a two-step reaction into thorium-232: 244 Pu ⟶ 236 U ⟶ 232 Th . ^{244}\text{Pu} \longrightarrow \,^{236}\text{U} \longrightarrow \,^{232}\text{Th}.
  • The half-lives of plutonium-244 and uranium-236 are 80 and 23 million years, respectively.
  • Thorium-232 is stable (half-life is longer than 10 billion years).


The answer is 99.

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Arjen Vreugdenhil
Oct 15, 2017

The decay can be described as a matrix differential equation d d t [ Pu U Th ] = [ − α 0 0 α − β 0 0 β 0 ] [ Pu U Th ] . \frac{d}{dt} \left[\begin{array}{c}\text{Pu} \\ \text{U} \\ \text{Th}\end{array}\right] = \left[\begin{array}{ccc}-\alpha & 0 & 0 \\ \alpha & -\beta & 0 \\ 0 & \beta & 0\end{array}\right] \ \left[\begin{array}{c}\text{Pu} \\ \text{U} \\ \text{Th}\end{array}\right]. Here, α = ln ⁡ 2 halflife of Pu ; β = ln ⁡ 2 halflife of U . \alpha = \frac{\ln 2}{\text{halflife of Pu}};\ \ \ \beta = \frac{\ln 2}{\text{halflife of U}}. In general, to solve a linear matrix differential equation of the form d x ⃗ / d t = M x ⃗ d\vec x/dt = M\:\vec x , we wish to find a basis for the vector space in which M M is diagonal. Then we simply apply d x ⃗ d t = [ λ 1 ⋱ λ n ] x ⃗ ; x ⃗ ( 0 ) = [ a 1 ⋮ a n ] ; ⟹ x ⃗ ( t ) = [ a 1 e λ 1 t ⋮ a n e λ n t ] . \frac{d\vec x}{dt} = \left[\begin{array}{ccc} \lambda_1 & & \\ & \ddots & \\ & & \lambda_n \end{array}\right]\ \vec x;\ \ \ \vec x(0) = \left[\begin{array}{c} a_1 \\ \vdots \\ a_n\end{array}\right];\ \ \ \Longrightarrow\ \ \ \vec x(t) = \left[\begin{array}{c} a_1\:e^{\lambda_1t} \\ \vdots \\ a_n\:e^{\lambda_n t} \end{array}\right]. So let's get to work. To find the eigenvalues, we solve 0 = det ( M − λ I ) = ∣ − α − λ 0 0 α − β − λ 0 0 β − λ ∣ = − ( α + λ ) ( β + λ ) λ . 0 = \text{det} (M - \lambda I) = \left|\begin{array}{ccc}-\alpha-\lambda & 0 & 0 \\ \alpha & -\beta-\lambda & 0 \\ 0 & \beta & -\lambda\end{array}\right| = -(\alpha+\lambda)(\beta+\lambda)\lambda. Thus the eigenvalues are λ 1 = − α ; λ 2 = − β ; λ 3 = 0 \lambda_1 = -\alpha;\ \lambda_2 = -\beta;\ \lambda_3 = 0 . The corresponding eigenvectors are e ⃗ 1 = [ β − α α − β ] ; e ⃗ 2 = [ 0 1 − 1 ] ; e ⃗ 3 = [ 0 0 1 ] . \vec e_1 = \left[\begin{array}{c} \beta - \alpha \\ \alpha \\ -\beta \end{array}\right];\ \ \ \vec e_2 = \left[\begin{array}{c} 0 \\ 1 \\ -1 \end{array}\right];\ \ \ \vec e_3 = \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right]. The original amounts may be written as [ Pu 0 U 0 Th 0 ] = [ 1 0 0 ] = a 1 [ β − α α − β ] + a 2 [ 0 1 − 1 ] + a 3 [ 0 0 1 ] ; \left[\begin{array}{c}\text{Pu}_0 \\ \text{U}_0 \\ \text{Th}_0\end{array}\right] = \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] = a_1\left[\begin{array}{c} \beta - \alpha \\ \alpha \\ -\beta \end{array}\right] + a_2 \left[\begin{array}{c} 0 \\ 1 \\ -1 \end{array}\right] + a_3 \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right]; it is not difficult to see that a 1 = 1 β − α , a 2 = − α β − α , a 3 = 1. a_1 = \frac{1}{\beta - \alpha},\ a_2 = \frac{-\alpha}{\beta - \alpha},\ a_3 = 1. Thus, translated to the eigenvalue bases, the process is now reduced to the diagonal form d x ⃗ d t = [ − α − β 0 ] x ⃗ ; x ⃗ ( 0 ) = 1 β − α [ 1 − α β − α ] \frac{d\vec x}{dt} = \left[\begin{array}{ccc} -\alpha & & \\ & -\beta & \\ & & 0 \end{array}\right]\ \vec x;\ \ \ \vec x(0) = \frac 1 {\beta - \alpha} \left[\begin{array}{c} 1 \\ -\alpha \\ \beta - \alpha \end{array}\right] with solution x ⃗ ( t ) = 1 β − α [ e − α t − α e − β t β − α ] . \vec x(t) = \frac 1 {\beta - \alpha} \left[\begin{array}{c} e^{-\alpha t} \\ -\alpha e^{-\beta t} \\ \beta - \alpha \end{array}\right]. Translated back to the original basis, we now have an explicit formula for the amounts of each substance : [ Pu U Th ] ( t ) = 1 β − α [ ( β − α ) e − α t α ( e − α t − e − β t ) β ( 1 − e − α t ) − α ( 1 − e − β t ) ] . \left[\begin{array}{c}\text{Pu} \\ \text{U} \\ \text{Th}\end{array}\right](t) = \frac 1{\beta - \alpha} \left[\begin{array}{c}(\beta - \alpha) e^{-\alpha t} \\ \alpha(e^{-\alpha t} - e^{-\beta t}) \\ \beta(1-e^{-\alpha t}) - \alpha(1-e^{-\beta t}) \end{array}\right].

To answer the question, we equate the amounts of plutonium and thorium: ( β − α ) e − α t = β ( 1 − e − α t ) − α ( 1 − e − β t ) ; 2.4035 ⋅ 2 − t / 80 − 0.4035 ⋅ 2 − t / 23 = 1. (\beta - \alpha)e^{-\alpha t} = \beta(1-e^{-\alpha t}) - \alpha(1-e^{-\beta t}); \\ 2.4035\cdot 2^{-t/80} - 0.4035\cdot 2^{-t/23} = 1. There is no simple algebraic solution; a numerical solution yields t ≈ 99 t \approx \boxed{99} million years.]

11 Helpful 0 Interesting 0 Brilliant 0 Confused

A single decay can be descripted by an exponential function N ( t ) = N 0 exp ⁡ ( − λ t ) N(t) = N_0 \exp(-\lambda t) with the initial number of atoms N 0 N_0 and the decay constant λ \lambda . The decay constant can be calculated from the half-life time: N 0 2 = N ( t 1 / 2 ) = N 0 exp ⁡ ( − λ t 1 / 2 ) ⇒ λ = ln ⁡ 2 t 1 / 2 \frac{N_0}{2} = N(t_{1/2}) = N_0 \exp(-\lambda t_{1/2}) \quad \Rightarrow \quad \lambda = \frac{\ln 2}{t_{1/2}} For a two-step decay we have a system of differential equations N ˙ Pu = − λ Pu N Pu N ˙ U = λ Pu N Pu − λ U N U N ˙ Th = λ U N U \begin{aligned} \dot N_\text{Pu} &= - \lambda_\text{Pu} N_\text{Pu} \\ \dot N_\text{U} &= \lambda_\text{Pu} N_\text{Pu} - \lambda_\text{U} N_\text{U} \\ \dot N_\text{Th} &= \lambda_\text{U} N_\text{U} \end{aligned} for the number of atoms N X N_X for X = Pu , U , Th X = \text{Pu}, \text{U}, \text{Th} . Initial conditions for t = 0 t = 0 are N Pu = N 0 , N U = N Th = 0 N_\text{Pu} = N_0, N_\text{U} = N_\text{Th} = 0 . The solution for N Pu N_\text{Pu} is a simple exponential decay: N Pu ( t ) = N 0 exp ⁡ ( − λ Pu t ) N_\text{Pu}(t) = N_0 \exp(-\lambda_\text{Pu} t) For uranium a general solution of the homogeneous equation N ˙ U + λ U N U = 0 ⇒ N U ∝ exp ⁡ ( − λ U t ) \dot N_\text{U} + \lambda_\text{U} N_\text{U} = 0 \quad \Rightarrow \quad N_\text{U} \propto \exp(-\lambda_\text{U} t) and a special solution of the inhomogeneous equation N ˙ U + λ U N U = λ Pu N Pu ⇒ N U ∝ exp ⁡ ( − λ Pu t ) \dot N_\text{U} + \lambda_\text{U} N_\text{U} = \lambda_\text{Pu} N_\text{Pu} \quad \Rightarrow \quad N_\text{U} \propto \exp(-\lambda_\text{Pu} t) can be found, so that the general solution is linear combination of both: N U ( t ) = A exp ⁡ ( − λ Pu t ) + B exp ⁡ ( − λ U t ) N ˙ U = − λ Pu A exp ⁡ ( − λ Pu t ) − λ U B exp ⁡ ( − λ U t ) λ Pu N Pu − λ U N U = ( λ Pu N 0 − λ U A ) exp ⁡ ( − λ Pu t ) − λ U B exp ⁡ ( − λ U t ) ⇒ A = λ Pu λ U − λ Pu N 0 N U ( 0 ) = A + B = ! 0 ⇒ B = − A = − λ Pu λ U − λ Pu N 0 \begin{aligned} & & N_\text{U}(t) &= A \exp(-\lambda_\text{Pu} t) + B \exp(-\lambda_\text{U} t) \\ & &\dot N_\text{U} &= - \lambda_\text{Pu} A \exp(-\lambda_\text{Pu} t) - \lambda_\text{U} B \exp(-\lambda_\text{U} t) \\ & & \lambda_\text{Pu} N_\text{Pu} - \lambda_\text{U} N_\text{U} &= (\lambda_\text{Pu} N_0 - \lambda_\text{U} A) \exp(-\lambda_\text{Pu} t) - \lambda_\text{U} B \exp(-\lambda_\text{U} t)\\ \Rightarrow & & A &= \frac{\lambda_\text{Pu}}{\lambda_\text{U} - \lambda_\text{Pu}} N_0 \\ & & N_\text{U}(0) &= A + B \stackrel{!}{=} 0 \\ \Rightarrow & & B &= -A = - \frac{\lambda_\text{Pu}}{\lambda_\text{U} - \lambda_\text{Pu}} N_0 \end{aligned} The number of thorium atoms can be found by integration: N Th ( t ) = λ U ∫ 0 t N U ( t ) d t = − λ U [ A λ Pu exp ⁡ ( − λ Pu t ) + B λ U exp ⁡ ( − λ U t ) ] 0 t = λ U N 0 λ U − λ Pu [ 1 − exp ⁡ ( − λ Pu t ) ] − λ Pu N 0 λ U − λ Pu [ 1 − exp ⁡ ( − λ U t ) ] = N 0 − N Pu ( t ) − N U ( t ) \begin{aligned} N_\text{Th}(t) &= \lambda_\text{U} \int_0^t N_\text{U}(t) dt = -\lambda_\text{U} \left[ \frac{A}{\lambda_\text{Pu}} \exp(-\lambda_\text{Pu} t) + \frac{B}{\lambda_\text{U}} \exp(-\lambda_\text{U} t) \right]_0^t \\ &= \frac{\lambda_\text{U} N_0}{\lambda_\text{U} - \lambda_\text{Pu}} [ 1 - \exp(-\lambda_\text{Pu} t) ] - \frac{\lambda_\text{Pu} N_0}{\lambda_\text{U} - \lambda_\text{Pu}} [ 1 - \exp(-\lambda_\text{U} t) ] \\ &= N_0 - N_\text{Pu}(t) - N_\text{U}(t) \end{aligned} 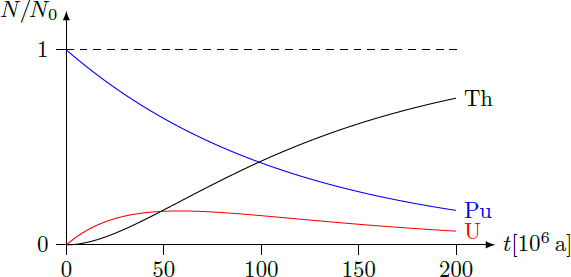A plot of the functions provides the graphical solution N Pu ( t ) = N Th ( t ) N_\text{Pu}(t) = N_\text{Th}(t) for the age t ≈ 99 ⋅ 1 0 6 a t \approx 99 \cdot 10^6 \,\text{a}

10 Helpful 0 Interesting 0 Brilliant 0 Confused

(freepascal)

program desintegration;

uses math;

var

cpr,ctr,ctr0,dt,a,b,c,alfa,beta,gamma:real; n:longint;

begin 

    alfa:=ln(2)/80000000;
    beta:=ln(2)/23000000;


    dt:=1000;             { step of time: 1000 years }
    a:=exp(-(dt*alfa));
    b:=exp(-(dt*beta));
    c:=dt*alfa;
    ctr0:=c*a/(1-a);

    gamma:=0;

    n:=0;

    while ctr<=cpr do

    begin


            cpr:=(1-c*(1- exp((n+1)*ln(a))  )/(1-a) ); {plutonium quantity after n thousands of years }

            gamma:=exp(n*ln(a))+b*(gamma);

            ctr:=ctr0*((1-exp((n+1)*ln(b)))-(1-b)*gamma); {Thorium quantity after n thousands of years }

            n:=n+1

    end;

    n:=round(n/1000);


    writeln(n); { number of thousands of years }

end.

Result: n=99

JUAN MANUEL CRUZ MORALES - 2 years, 1 month ago

great problem, sir !

André Hucek - 3 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...