Hunt it or it will haunt you!

Let the $\odot ADB \cap AC \equiv O.$ Now, $AO$ is the bisector of $\angle ADB$ , therefore, $AO$ bisects arc $BD$ and $BO = DO$ . Also, $\angle DOB = 70^{\circ} =>$ $O$ is the circumcenter of $\Delta DBC$ .

Clearly, $\angle AOD + \angle DOC = \angle ABD + 2 \times \angle DBC = \angle ABD + 2 \times [\angle 110^{\circ} - \angle ABD] = 180^{\circ} => \angle ABD = 40^{\circ}$

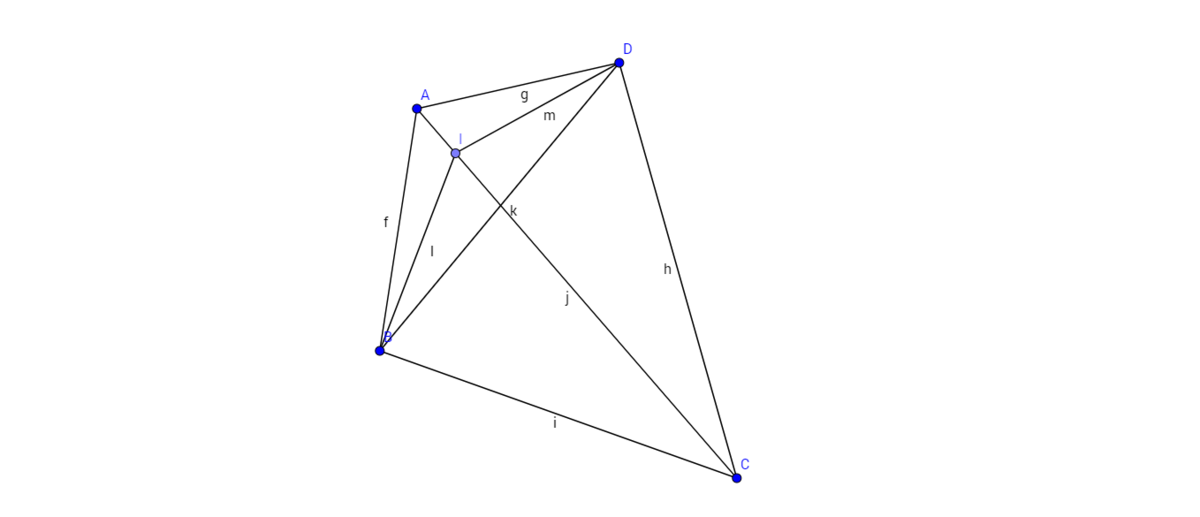
Let $I$ be the Incenter of $\triangle ABD$ and $\angle ABD=2x.$ $\angle BID=90+\dfrac{\angle A}{2}=145^\circ.$ We can clearly see that Quad. $BIDC$ is cyclic since $\angle BID+\angle BCD=145^\circ+35^\circ=180^\circ.$ By angle chasing we know that $\angle ACD=20^\circ=\angle DBI$ by cyclic properties. Therefore $\angle ABD=2\times 20^\circ=\boxed{40^\circ}.$