Angle addition
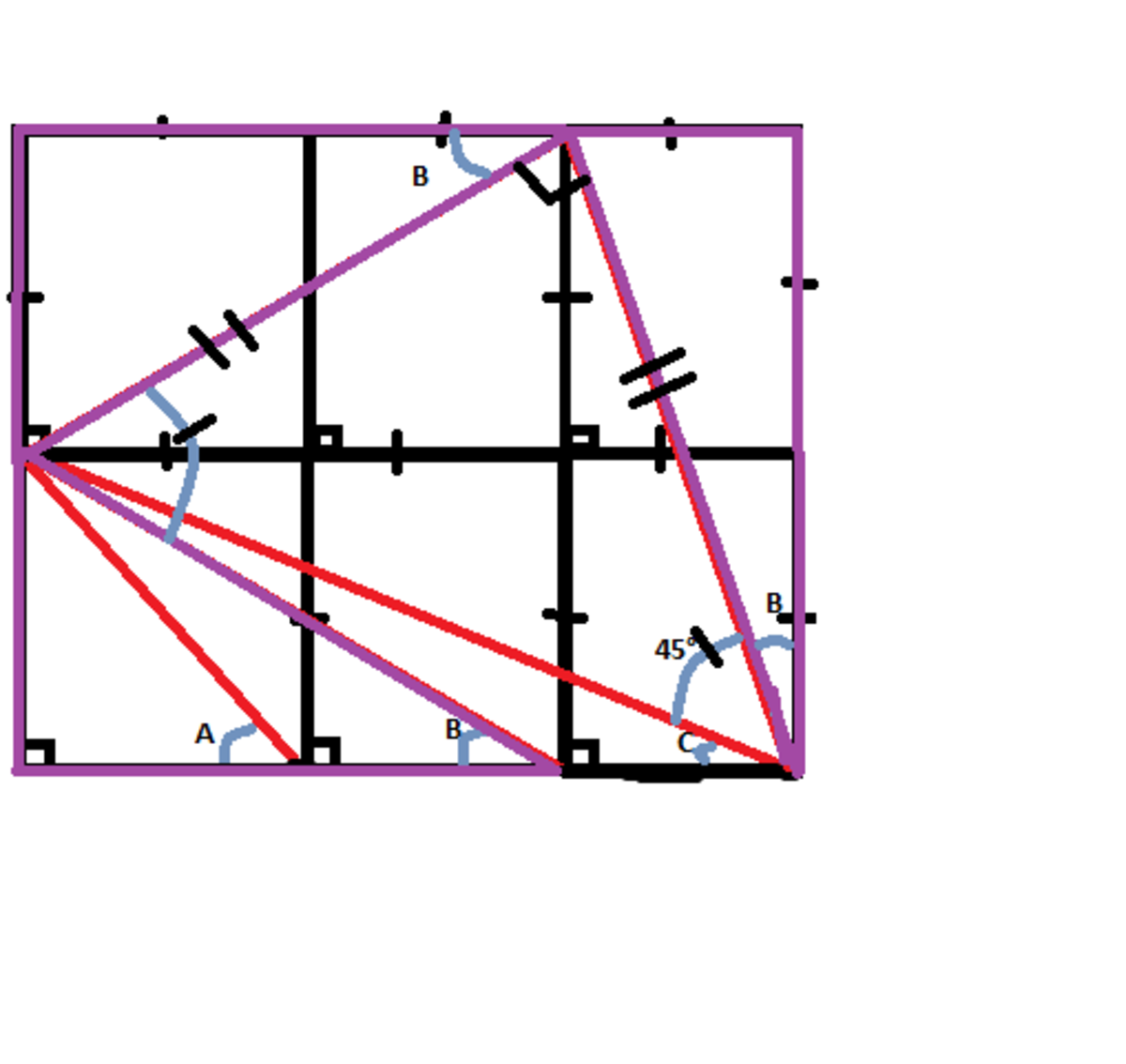
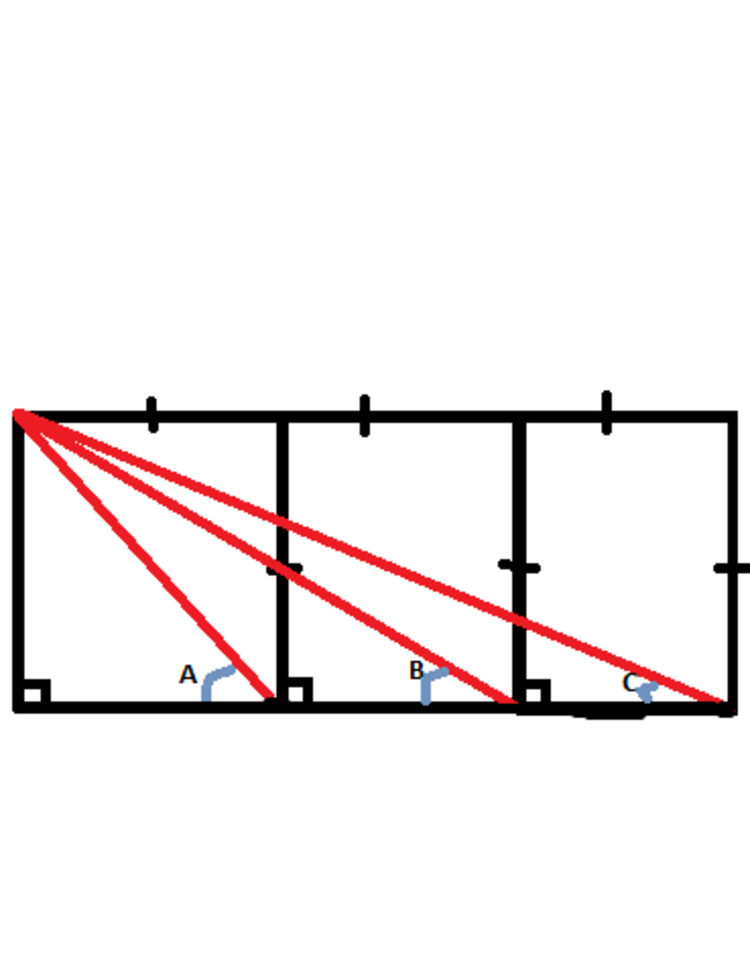 The above rectangle is divided into 3 congruent squares. The angles A, B and C are defined by the sides of the rectangle and the red segments.
The above rectangle is divided into 3 congruent squares. The angles A, B and C are defined by the sides of the rectangle and the red segments.
A+B+C=X
Find X
(Answer is in degrees, does not require °)
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.