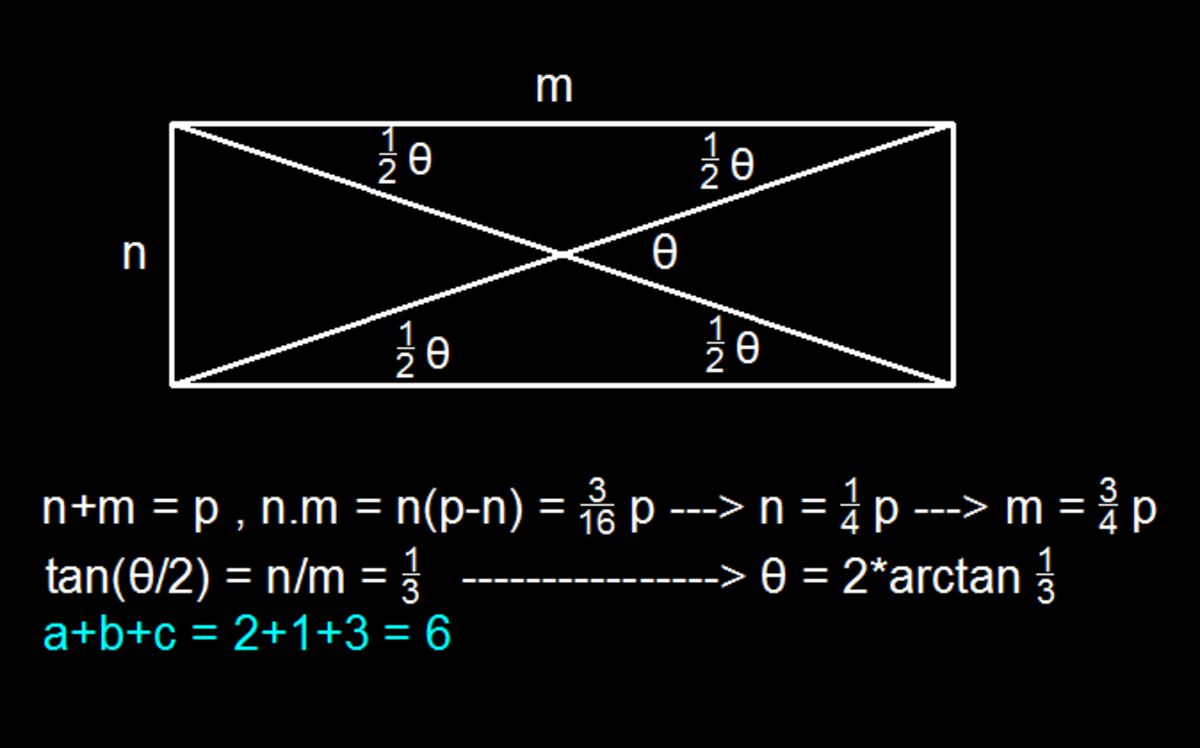
Angle Between Diagonals?
Find the acute angle θ between the diagonals of a rectangle with perimeter 2 p and area 1 6 3 p 2 .
If θ = a tan − 1 ( c b ) , where a , b , c are coprime positive integers, then enter the value of a + b + c .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
A typo first line
N
O
T
1
6
3
∗
p
b
u
t
1
6
3
∗
p
2
.
A different approach is as under with the same diagram above but not for the given condition.
m
+
n
=
p
,
m
∗
n
=
1
6
3
p
2
.
∴
D
i
a
g
o
n
a
l
2
=
m
2
+
n
2
=
(
m
+
n
)
2
−
2
∗
m
∗
n
=
8
5
∗
p
2
.
⟹
H
a
l
f
D
i
a
g
o
n
a
l
,
(
H
D
)
=
2
1
∗
8
5
∗
p
2
.
∴
A
r
e
a
,
4
A
o
f
q
u
a
r
t
e
r
r
e
c
t
a
n
g
l
e
=
2
1
∗
(
H
D
)
2
∗
S
i
n
θ
∴
A
=
4
∗
8
1
∗
8
5
∗
p
2
∗
S
i
n
θ
=
1
6
3
p
2
.
.
.
g
i
v
e
n
.
∴
S
i
n
θ
=
5
3
,
i
m
p
l
i
e
s
T
a
n
θ
=
4
3
.
∴
1
∗
T
a
n
−
1
4
3
.
=
a
∗
T
a
n
−
1
c
b
,
s
i
n
c
e
a
i
s
n
o
t
c
o
−
p
r
i
m
e
+
t
i
v
e
i
n
t
e
g
e
r
.
T
h
o
u
g
h
t
1
∗
T
a
n
−
1
4
3
=
2
∗
T
a
n
−
1
3
1
.
.
Nice Solution ( + 1 ) !