Angle between tangents to an ellipse
An ellipse is given by
4 x 2 + y 2 = 1
From the point
(
4
,
3
)
the two possible tangents to the ellipse are drawn. Find the angle (in degrees) between the two tangents. Round your answer to the nearest tenth of a degree.
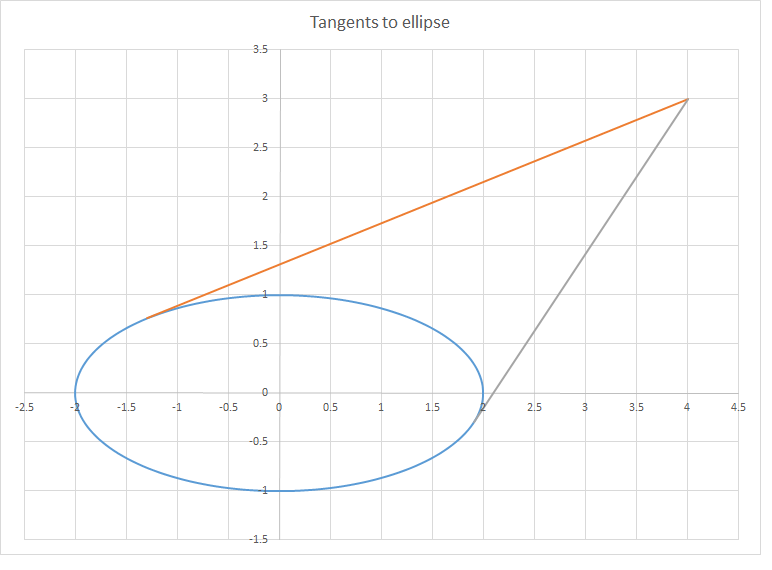
The chart provided is drawn to scale.
The answer is 34.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the equation of tangent(slope 'm') be y-3=m(x-4) or y=mx+3-4m.Applying condition of tangency, we get ( 3 − 4 m ) 2 = 4 m 2 + 1 ⇒ 3 m 2 − 6 m + 2 = 0 , m 1 + m 2 = 2 , m 1 m 2 = 2 / 3 θ = tan − 1 ( 1 + m 1 m 2 m 1 − m 2 ) = tan − 1 5 2 3 = 3 4 . 7 °
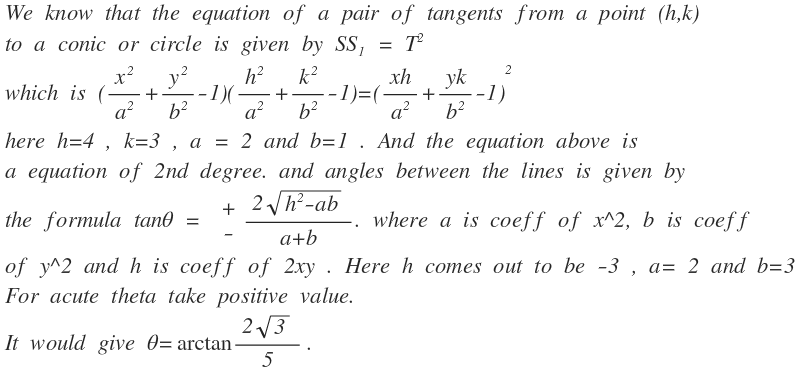
The ellipse is given by:
x 2 / a 2 + y 2 / b 2 = 1
with a = 2 and b = 1 . The gradient at any point ( x , y ) on the ellipse is given by:
g = ( 2 x / a 2 , 2 y / b 2 )
The given point from which the tangents are drawn is: ( x 0 , y 0 ) , with x 0 = 4 , y 0 = 3 .
Now, the condition for tangency is
g . ( x − x 0 , y − y 0 ) = 0
Hence
2 ( x − x 0 ) / a 2 + 2 y ( y − y 0 ) / b 2 = 0
which, upon simplifying, becomes
x x 0 / a 2 + y y 0 / b 2 = 1
Now, we substitute this in ellipse equation:
x 2 / a 2 + ( ( b 2 / y 0 ) 2 ( 1 − x x 0 / a 2 ) 2 / b 2 = 1
Expanding,
x 2 / a 2 + b 2 / y 0 2 ( 1 − 2 x x 0 / a 2 + x 2 x 0 2 / a 4 ) = 1
which is of the form,
a 2 x 2 + a 1 x + a 0 = 0
with
a 2 = ( 1 / a 2 ) + ( x 0 2 / y 0 2 ) ( b 2 / a 4 ) = ( 1 / a 2 ) ( 1 + ( x 0 / y 0 ) 2 ( b / a ) 2 )
a 1 = − 2 ( x 0 / y 0 2 ) ( b / a ) 2
a 0 = b 2 / y 0 2 − 1
So now, we can solve the quadratic equation for x, then solve for y from x x 0 / a 2 + y y 0 / b 2 = 1
Having found the two solution points (x1, y1) and (x2, y2) we can determine the gradients at each point as
g 1 = ( 2 x 1 / a 2 , 2 y 1 / b 2 )
g 2 = ( 2 x 2 / a 2 , 2 y 2 / b 2 )
Now, it is straight forward to find the angle between the two gradients, and to find the angle between the two tangents, we subtract this found angle from 180.
Substituting the given values of a , b , x 0 , y 0 , we obtain the following tangency points:
( − 1 . 2 9 1 , 0 . 7 6 4 ) and ( 1 . 9 0 7 , − 0 . 3 0 2 )
From which the angle is computed as explained above, it comes to 3 4 . 7 .