Angle between the circles.
Geometry
Level
4
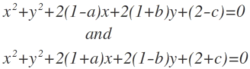 Find (a,b) such that the circles cut orthogonally.
Find (a,b) such that the circles cut orthogonally.
None Of these
(0,1)
(1,0)
(0,0)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For two circles, x 2 + y 2 + 2 g 1 x + 2 f 1 y + c 1 = 0 and x 2 + y 2 + 2 g 2 x + 2 f 2 y + c 2 = 0 , to be orthogonal, the following condition must be satisfied.
2 g 1 g 2 + 2 f 1 f 2 = c 1 + c 2
On applying the above condition, we get a 2 + b 2 = 0 .
this implies a = b = 0
But these values of a and b make the circles concentric. Hence there is no actual intersection of the circles possible which may make them orthogonal.