Angle between two surfaces!
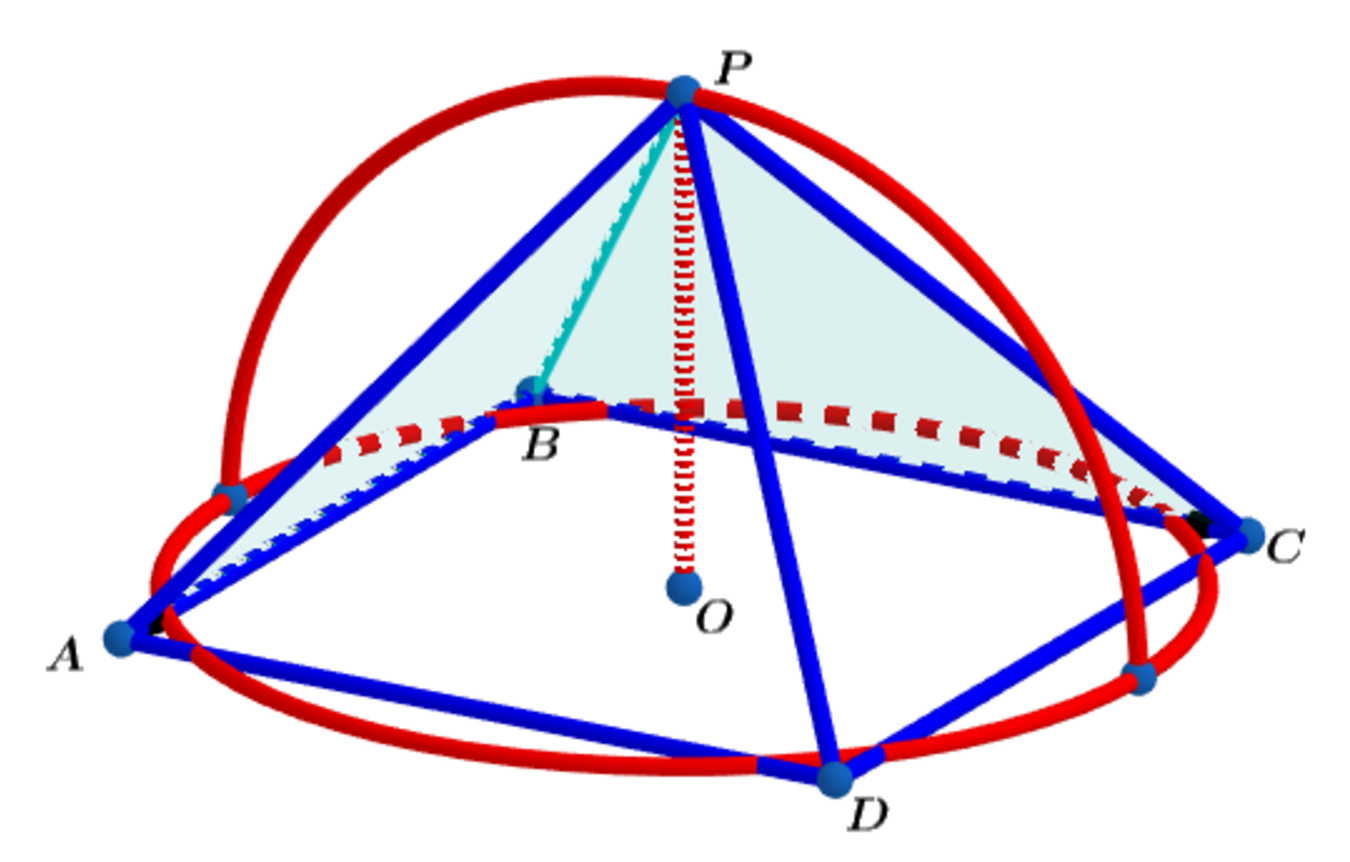
Let O be the center of square A B C D and construct a circle centered at O whose circumference is equal to the perimeter of the square. Folding the arc of the semi-circle at a right angle, as shown above, the radius of the semicircle becomes the height of the right square pyramid.
Find the acute angle made between two adjacent faces (in degrees).
The answer is 67.57253352.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
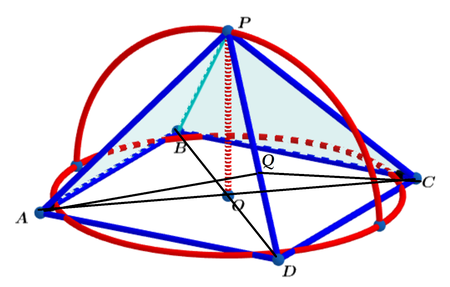
Let point Q on P D be such that A Q and C Q are perpendicular to P D . Then ∠ A Q C = θ is the angle between the two faces of the pyramid.
Let the common perimeter be 2 π . Then the radius or the height O P = 1 and the side length the square A B C D is 2 π , B D = 2 π , O D = 2 2 π , and P D = O P 2 + O D 2 = 1 + 8 π 2 . cos ∠ P D A = P D 2 1 A D = 1 6 + 2 π 2 π ⟹ sin ∠ P D A = 1 6 + 2 π 2 1 6 + π 2 . And we have:
sin 2 θ ⟹ θ = A Q A O = A D sin ∠ P D A A O = 3 2 + 2 π 1 6 + 2 π 2 = 2 sin − 1 3 2 + 2 π 1 6 + 2 π 2 ≈ 1 1 2 . 4 2 7 4 6 6 4 7 7 ∘
Therefore the acute angle between the two faces is 1 8 0 ∘ − 1 1 2 . 4 2 7 4 6 6 4 7 7 ∘ ≈ 6 7 . 6 ∘ .
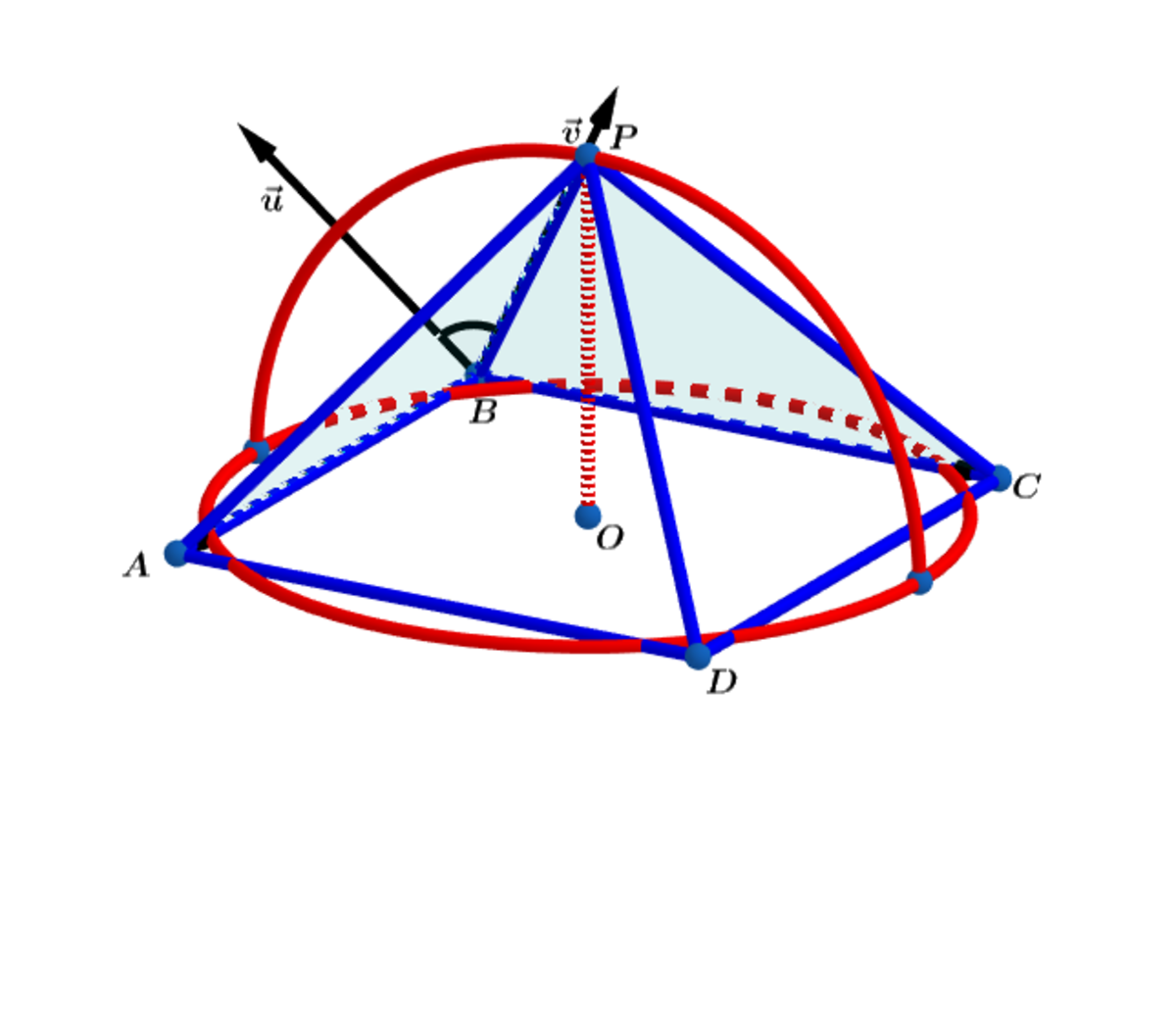
Let a be side of square base A B C D and r radius of the circle.
Let O ( 0 , 0 , 0 ) , A : ( − 2 a , − 2 a , 0 ) , B : ( − 2 a , 2 a , 0 ) , C : ( 2 a , 2 a , 0 ) , D : ( 2 a , − 2 a , 0 ) and P ( 0 , 0 , r )
B A = 0 i + a j + 0 k , B P = 2 a i + − 2 a j + r k and B C = a i + 0 j + 0 k
⟹ u = B P X B A = − a r i + 0 j + 2 a 2 k and v = B P X B C = 0 i + a j + 2 a 2 k
⟹ u ⋅ v = 4 a 4 = 4 4 a 2 r 2 + a 4 4 4 a 2 r 2 + a 4 cos ( θ ) = 4 4 a 2 r 2 + a 4 cos ( θ ) ⟹
4 a 4 = 4 a 2 ( 4 r 2 + a 2 ) cos ( θ ) ⟹ cos ( θ ) = 4 r 2 + a 2 a 2
and 4 a = 2 π r ⟹ r = π 2 a ⟹ cos ( θ ) = 1 6 + π 2 π 2 ⟹ θ = arccos ( 1 6 + π 2 π 2 ) ≈ 6 7 . 5 7 2 5 3 3 5 2 ∘ .
Nice question and solution! You may want to specify that you want the acute angle between the adjacent faces (and not the obtuse angle).
Thanks. I added acute angle.
Let E is mid point of AD, F at lateral edge PD and A F ⊥ P D , C F ⊥ P D . Then θ = ∠ A F C is dihedral angles of adjacent faces. Side length of square is a , radius of circle is r :
2 π r P E P D S △ P A D ∴ A F C F A C 2 ∴ cos θ θ = 4 a ⟹ r = π 2 a = r 2 + ( 2 a ) 2 = r 2 + 4 a 2 = r 2 + ( 2 2 a ) 2 = r 2 + 2 a 2 = 2 1 A D × P E = 2 1 A F × P D = P D A D × P E = r 2 + 2 a 2 a r 2 + 4 a 2 = A F = A F 2 + C F 2 − 2 ⋅ A F ⋅ C F ⋅ cos θ = 2 A F 2 − 2 A F 2 cos θ = 2 A F 2 A C 2 − 2 A F 2 = 2 A F 2 A C 2 − 1 = r 2 + 2 a 2 2 a 2 ( r 2 + 4 a 2 ) 2 a 2 − 1 = 4 r 2 + a 2 4 r 2 + 2 a 2 − 1 = 4 r 2 + a 2 a 2 = 4 ( π 2 ) 2 a 2 + a 2 a 2 = 1 6 + π 2 π 2 = cos − 1 1 6 + π 2 π 2 ≈ 6 7 . 5 7 °
Let the sides of the square be l and let the radius of the circle (and the height of the pyramid) be h .
Since the circle's circumference is equal to the perimeter of the square, 4 l = 2 π h , or h = π 2 l .
The acute dihedral angle of a square pyramid with a base side of l and a height of h is:
θ = cos − 1 ( l 2 + 4 h 2 l 2 ) = cos − 1 ( l 2 + 4 ( π 2 l ) 2 l 2 ) = cos − 1 ( π 2 + 1 6 π 2 ) ≈ 6 7 . 5 7 2 5 3 3 5 2 °