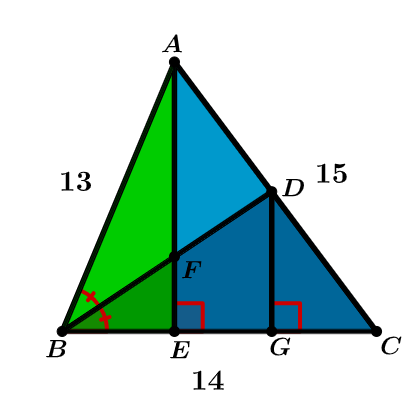
Angle Bisector and Altitude

Geometry Level 3

If A B = 13 AB = 13 , B C = 14 BC = 14 , and A C = 15 AC = 15 , D F DF can be written in the form a b c \frac{a\sqrt{b}}{c} , where a a and c c are coprime, positive integers and b b is square-free. What is a + b + c a+b+c ?


The answer is 35.

Aidan Poor by Aidan Poor , 18, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Aidan Poor
Oct 7, 2018

Hint: Angle Bisector Theorem and similar triangles.

2 Helpful 1 Interesting 0 Brilliant 1 Confused

Please post the complete solution

Bivab Mishra - 2 years, 8 months ago
Ajit Athle
Oct 9, 2018

We can begin with the fact that, BE=5 & EC=9 and BD²= 14*13(1- 15 ² 27 ² \frac{15²}{27²} ) or BD= 28 √ 13 9 \frac{28√13}{9} . Also, C D D A \frac{CD}{DA} = 14 13 \frac{14}{13} or C A A D \frac{CA}{AD} = 27 13 \frac{27}{13} . Using Menelaus's Theorem in Tr. BDC with AFD as the transversal, [ B E E C \frac{BE}{EC} ][ C A A D \frac{CA}{AD} ][ D L L B \frac{DL}{LB} ]=1 which yields, D L L B \frac{DL}{LB} = 13 15 \frac{13}{15} or D L B D \frac{DL}{BD} = 13 28 \frac{13}{28} . Then DL = 13 √ 13 9 \frac{13√13}{9}

0 Helpful 0 Interesting 0 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...