Angle bisector length
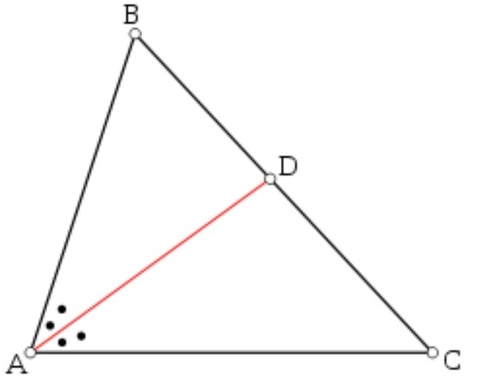In triangle
A
B
C
, if
A
B
=
1
0
,
A
C
=
1
6
,
C
D
=
8
, and
A
D
bisects angle
B
A
C
, find the length of
A
D
.
Image: courtesy of Wikipedia.
The answer is 10.954.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
See diagram, created by folding the triangle at line A D
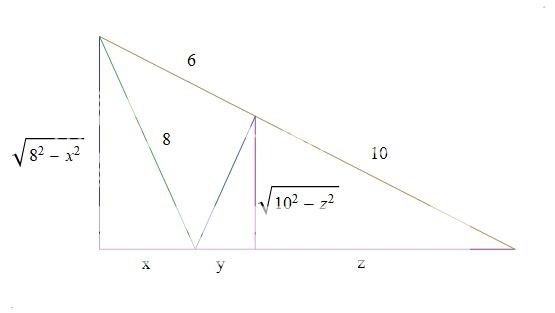Bisector
For the unknowns
x
,
y
,
z
, we have the following proportional equations
z 1 0 = x + y + z 1 6
z 1 0 2 − z 2 = x + y + z 8 2 − x 2
y 1 0 2 − z 2 = x 8 2 − x 2
Solve to get y + z = 2 3 0 , which is the exact answer.
i did it by using stewart's theorem and relation of angle bisectors with the sides of a triangle
The answer is 10.954 like it's show after congratulations menu!?:). Sorry! I have mistake. I think that the correct answer is 2sqrt{30} too. It's enough to find BD=5 from the properties of proportion of the angle bisector. Then sqr(AD) = AC.AB - DC.BD. The last condition is easy follow from the Stewart's theorem or from the properties of the chords in a circle which is circumscribes around the triangle ABC.
solved it using cosine rule and sine rule(actually angle bisector theorem)!
Log in to reply
@Kartik Sharma Can you show me how you solve it using the cosine rule, sine and the angle bisctor theorm
@Kartik Sharma can you please show how?
Log in to reply
Well, that's nothing new. It was a year ago when I solved it. Back then, I didn't know about Stewart's Theorem theorem and Angle Bisector Theorem(well, I did know this but didn't use it, hence in brackets). Both of these theorems are just simple facts we can get very easily from cosine and sine rule. So, I used these theorems(as others have done) without knowing of them.
The angle bisector theorem states that: A C A B = C D B D Let BD = x: 1 6 1 0 = 8 5 = 8 x ⇒ x = 5 Now if we let b and c be the sides adjacent to the bisected and a be the opposite side then the length of AD = d is given by d 2 = ( b + c ) 2 b c ( ( b + c ) 2 − a 2 ) ( 1 ) ( A D ) 2 = 2 6 2 1 0 × 1 6 ( 2 6 2 − 1 3 2 ) = 1 2 0 ∴ A D = 2 3 0 ≈ 1 0 . 9 5 Note that (1) is not the result of previous steps, rather it is a theorem.
In any triangle, x²= bc((b+c)²-a²)/(b+c)² where x = length of angle bisector from A and a, b, c have their usual meanings. https://proofwiki.org/wiki/Length of Angle_Bisector We've a = 13, b=16 & c=10. On substitution, we obtain, x=AD=2√30 ~= 10.9545
I did a bit of coordinate geometry.
By angle bisector theorem, we get BD=5
Let C(0,0)
D(8,0)
and B(13,0)
Let A(x,y)
Then AC=16 gives x²+y²=256
AB=10 gives (x-13)²+y²=100
Subtracting gives x=12.5 and y²=99.75
AD=√(x-8)²+y² = √120 ≈ 10.954