Angle Challenge
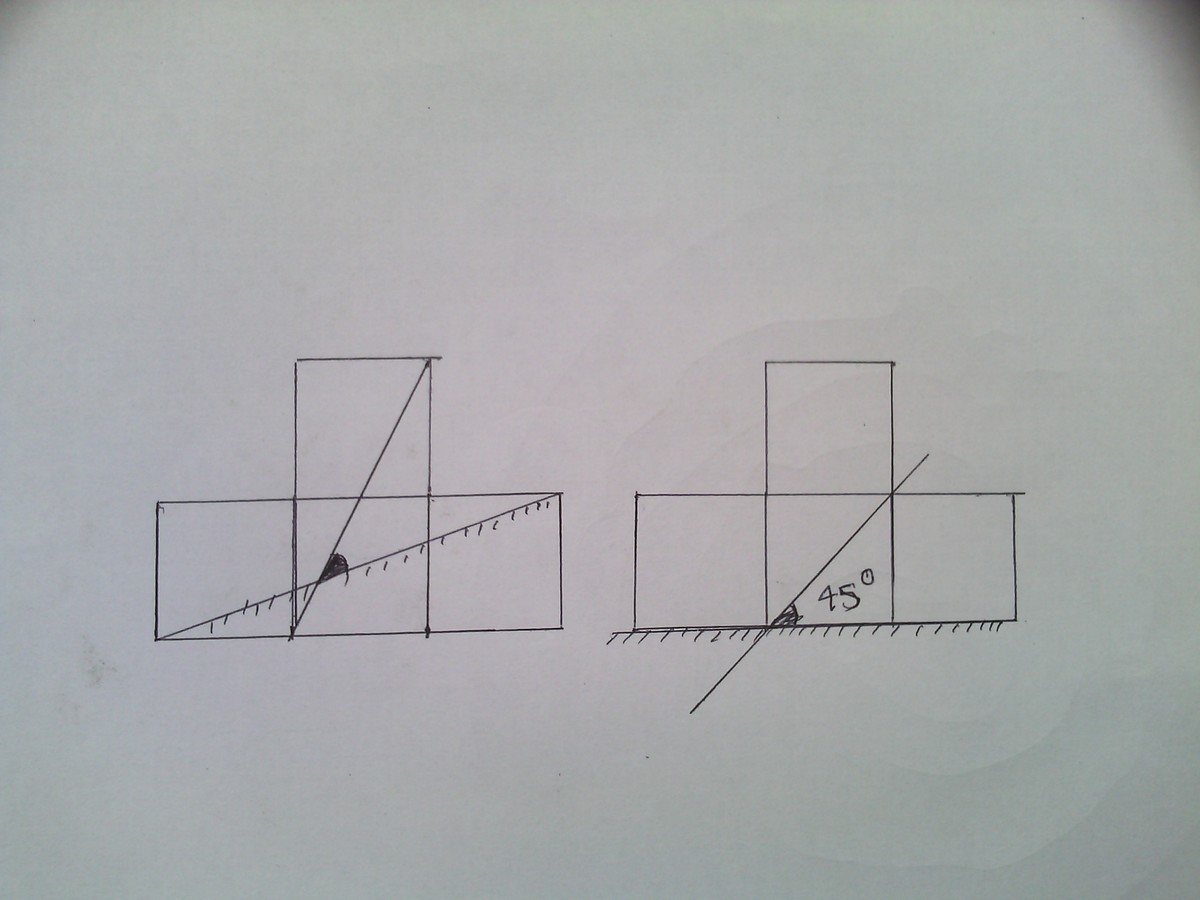
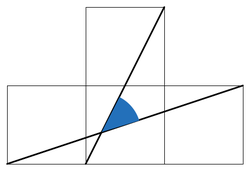The following figure is composed of congruent squares. Find the value of the blue angle (in degrees).
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
@Brian Charlesworth That's a very nice visualization! I've converted the comment into a solution, and added in an image for you :)
The triangle is clearly an isosceles one, having the sides the hypotenuses of two congruent right angle triangles.Also the triangle is right angle triangle,so the blue angle is 45 degrees.
Great idea!!!
That's a very nice application of
tan − 1 1 + tan − 1 2 1 + tan − 1 3 1 = 9 0 ∘ .
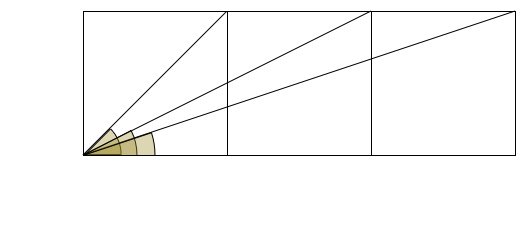
Is it cheating to use the arctan sum formula? We would just have
θ = arctan ( 2 ) − arctan ( 3 1 ) = arctan ( 1 + 2 ∗ 3 1 2 − 3 1 ) = arctan ( 1 ) = 4 5 ∘ .
Log in to reply
I've added an image to explain where I was coming from. I saw the relation to the image, which was a common problem asking to show that the sum of the three angles is 9 0 ∘ .
There are multiple ways of doing so. Arctan formula is a direct way, but there are other geometric approaches too which don't require knowledge of trigonometry.
@Maxwell Feiner Loved this question!
Log in to reply
Isn't it 180 degrees?
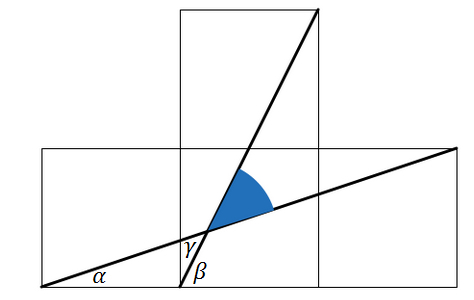
Let the sides length of the squares is 1, so we have:
sin β = 5 2 , cos β = 5 1 , sin α = 1 0 1 , and cos α = 1 0 3 .
Note that γ = β − α
sin γ = sin β cos α − cos β sin α = 5 2 1 0 3 − 5 1 1 0 1 = 5 2 5 = sin 4 5 ∘ (since γ is an acute angel)
Thus, γ = 4 5 ∘
It's simplest with trig, but this can be solved with some basic geometry... Here's a solution without words. Can someone fill in the details? :)
How I visualized it geometrically was to "shift" the slope 2 line segment to the left by one unit, and then join its uppermost vertex to the rightmost vertex of the slope 3 1 line segment to form an isosceles triangle with sides of length 5 , 5 and 1 0 = 2 5 , (assuming unit squares). The side ratios are then of the form 1 : 1 : 2 , and thus the triangle is a right isosceles triangle, implying that θ = 4 5 ∘ .
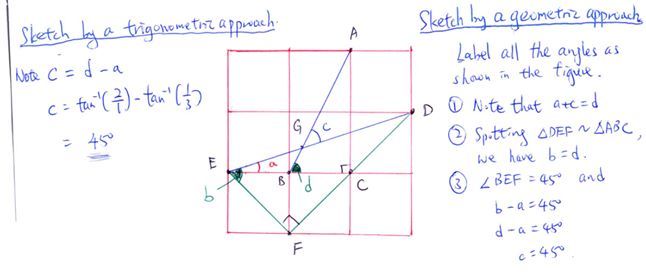Here is my drafted solution. Have fun.
Draw the diagram to scale and adjust the angle so that the lower end coincides with base,then the upper end becomes the diagonal of the square as shown then angle is 45
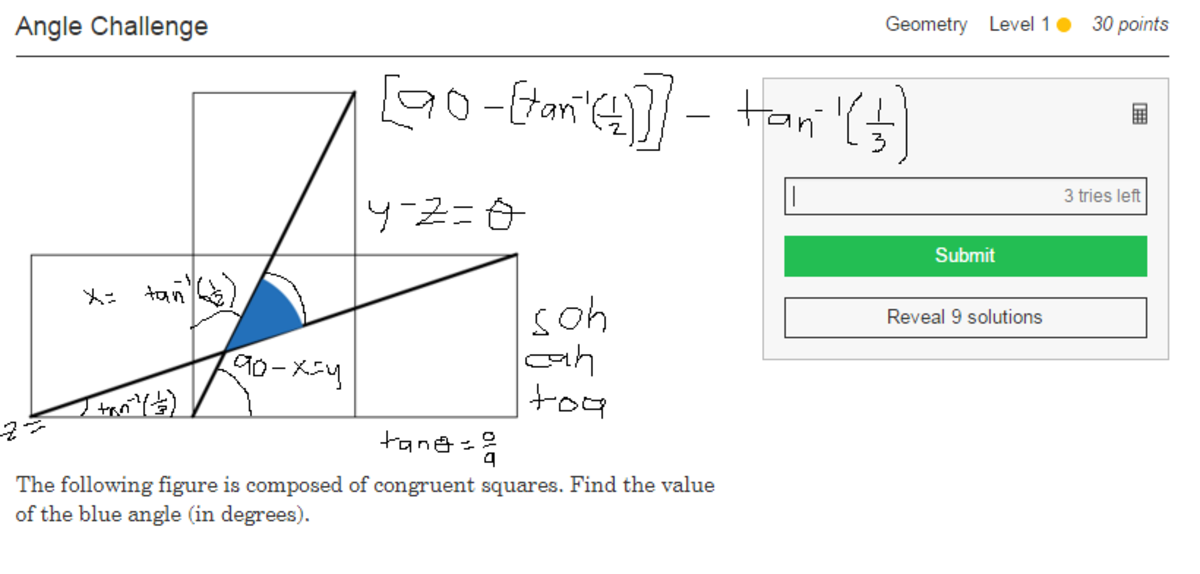
180 - (arctan(1/3) + arctan(1/2) + 90) = 45, but I'm more a fan of your basic geometry solutions!
How I interpreted this problem is that I thought how many degrees are in a square, which is 180 then afterwards I divided 180 to how many squares there were in the figure which is 4.. 180 divided by 4= 45
a circle can be drawn. required angle = 1/2 * 90
How i visualized is the other side was 135° and we know that 180° - 135° = 45° strange but that's the simplest fact.
The slope of the steeper line (let this be line 2) is 2. The slope of the other line (let this be line 1) is 1/3. Using the formula for angle between two lines in analytic geometry: tan A = (m2 - m1) / (1+ m2 x m1), we can compute that A is 45 degrees.
I drew the diagram in autocad and let the program do the math :p after getting the answer wrong twice on my own of course
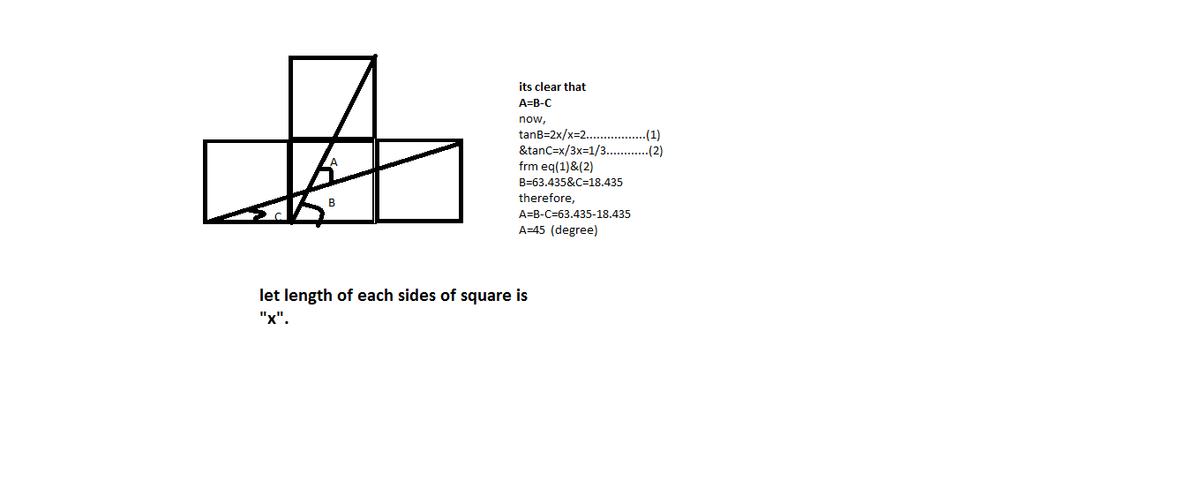
How I visualized it geometrically was to "shift" the slope 2 line segment to the left by one unit, and then join its uppermost vertex to the rightmost vertex of the slope 3 1 line segment to form an isosceles triangle with sides of length 5 , 5 and 1 0 = 2 5 , (assuming unit squares). The side ratios are then of the form 1 : 1 : 2 , and thus the triangle is a right isosceles triangle, implying that θ = 4 5 ∘ .