angle chaser

Geometry Level 3

The figure shows an isosceles right triangle ABC at B . AC = 2 , an other two lines AE & AD are drawn such that one of them is a median line ( ie bisect the opposite line CB) , and the other line is the angle bisector of angle A . the angle between the two lines AE and AD is α , if tan α = √p -√q , where p and q are positive integers , then find the value of p – q .


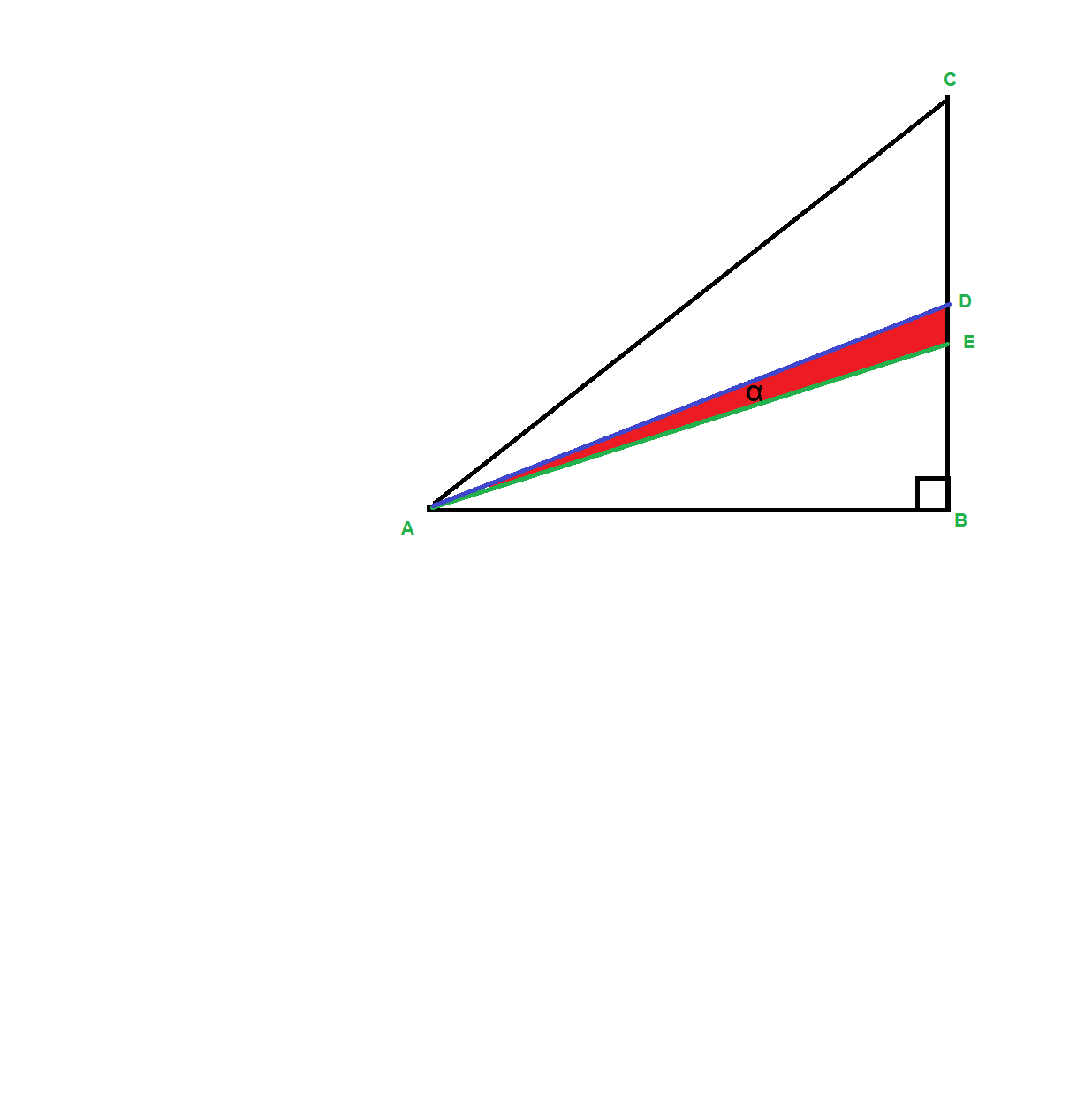
The answer is 1.

Aziz Alasha by Aziz Alasha , 59, Sudan

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Vreken
Sep 11, 2018

As an isosceles right triangle, ∠ C A B = 180 ° − 90 ° 2 = 45 ° \angle CAB = \frac{180° - 90°}{2} = 45° , so the angle bisector A E AE makes ∠ E A B = 45 ° 2 \angle EAB = \frac{45°}{2} , and the median A D AD makes ∠ D A B = tan ⁡ − 1 1 2 \angle DAB = \tan^{-1} \frac{1}{2} .

Therefore, α = tan ⁡ − 1 1 2 − 45 ° 2 \alpha = \tan^{-1} \frac{1}{2} - \frac{45°}{2} and tan ⁡ α = tan ⁡ ( tan ⁡ − 1 1 2 − 45 ° 2 ) \tan \alpha = \tan(\tan^{-1} \frac{1}{2} - \frac{45°}{2}) .

Using the tangent addition formula, tan ⁡ α = tan ⁡ ( tan ⁡ − 1 1 2 ) − tan ⁡ ( 45 ° 2 ) 1 + tan ⁡ ( tan ⁡ − 1 1 2 ) tan ⁡ ( 45 ° 2 ) \tan \alpha = \frac{\tan(\tan^{-1} \frac{1}{2}) - \tan(\frac{45°}{2})}{1 + \tan(\tan^{-1} \frac{1}{2})\tan(\frac{45°}{2})} = = 1 2 − tan ⁡ ( 45 ° 2 ) 1 + 1 2 tan ⁡ ( 45 ° 2 ) \frac{\frac{1}{2} - \tan(\frac{45°}{2})}{1 + \frac{1}{2}\tan(\frac{45°}{2})} .

Using the tangent half-angle formula, tan ⁡ ( 45 ° 2 ) = 1 − cos ⁡ 45 ° sin ⁡ 45 ° = 1 − 2 2 2 2 = 2 − 1 \tan(\frac{45°}{2}) = \frac{1 - \cos 45°}{\sin 45°} = \frac{1 - \frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = \sqrt{2} - 1 .

Substituting tan ⁡ ( 45 ° 2 ) = 2 − 1 \tan(\frac{45°}{2}) = \sqrt{2} - 1 into tan ⁡ α = 1 2 − tan ⁡ ( 45 ° 2 ) 1 + 1 2 tan ⁡ ( 45 ° 2 ) \tan \alpha = \frac{\frac{1}{2} - \tan(\frac{45°}{2})}{1 + \frac{1}{2}\tan(\frac{45°}{2})} gives tan ⁡ α = 1 2 − ( 2 − 1 ) 1 + 1 2 ( 2 − 1 ) ) \tan \alpha = \frac{\frac{1}{2} - (\sqrt{2} - 1)}{1 + \frac{1}{2}(\sqrt{2} - 1))} which simplifies to tan ⁡ α = 5 2 − 7 = 50 − 49 \tan \alpha = 5 \sqrt{2} - 7 = \sqrt{50} - \sqrt{49} .

Therefore, p = 50 p = 50 and q = 49 q = 49 and p − q = 1 p - q = \boxed{1} .

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Why does the median make angle DAB as tan inverse 1/2 ?

Anurag Bisht - 2 years, 8 months ago

Log in to reply

As an isosceles triangle, A B = B C AB = BC , and as a median, D B = 1 2 B C = 1 2 A B DB = \frac{1}{2}BC = \frac{1}{2}AB . So tan ⁡ ∠ D A B = D B A B = 1 2 A B A B = 1 2 \tan \angle DAB = \frac{DB}{AB} = \frac{\frac{1}{2}AB}{AB} = \frac{1}{2} .

David Vreken - 2 years, 8 months ago

Log in to reply

Got It! Thanks!

Anurag Bisht - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...