Angle of triangle in a circle

$This~ is ~a~ more~ clear~ and~ prominent~ solution.$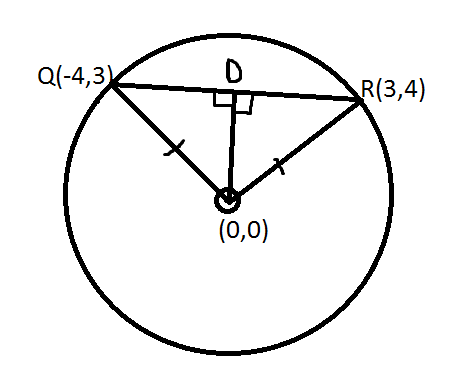
Since , $x^2+y^2=25$ ,

Hence, $radius~=~5~units$

Construct $OD$ as perpendicular from $~O~to~QR$

Again, $\triangle QOD~ and~ \triangle ROD$ are congruent

Thus , $QD~=~DR$

Distance between $QR~=~\sqrt{(-4-3)^2+(3-4)^2}$

$QR~=~5\sqrt{2}~units$

Thus, $QD~=~\frac{5\sqrt{2}}{2}$

Now in $\triangle QOD$

$sin \angle QOD~=~\large\frac{\frac{5\sqrt{2}}{2}}{5}$

$sin \angle QOD~=~\frac{\sqrt{2}}{2}$

Therefore $\angle QOD~=~45$

$\angle QOR~=~2 \times 45~=~90$

$\angle{QPR}~=~\frac{90}{2}$ [Since angle subtended by a chord at circumference is half the angle subtended by it at the center]

$\boxed {\angle{QPR}~=~45}$

Let O be center of circle (origin). Let C be point ( - 4, 0) and D be point (3,0).

Angle QOC = arctan(3/4) = 36.87 degrees. Angle ROD = arctan(4/3) = 53.13 degrees.

Since COD is straight line, Angle QOR = 180 - 36.87 - 53.13 = 90 degrees.

Angle QOR cuts Arc QR which is also 90 degrees.

Therefore, Angle QPR, where P is * any * point on Arc QPR , = 1/2 of Arc QR = 1/2 * 90 = 45 degrees.