Angle of view
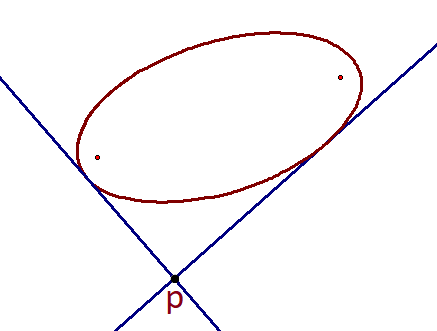
What shape is formed by the set of all points where two tangents to a non-circular ellipse are perpendicular?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The set of all points p where two tangents are perpendicular for any conic is an orthoptic , and the orthoptic for an ellipse in the form of a 2 x 2 + b 2 y 2 = 1 is a circle with the equation x 2 + y 2 = a 2 + b 2 .
Proof: Using implicit differentiation on a 2 x 2 + b 2 y 2 = 1 gives a 2 2 x + b 2 2 y y ′ = 0 , which simplifies to y ′ = − a 2 y b 2 x , and is the slope of the curve m = y ′ at any point ( x , y ) . Let ( p , q ) and ( r , s ) be points on the ellipse such that their tangent are perpendicular. Then the equation of the tangent line at a point ( p , q ) is y − q = − a 2 q b 2 p ( x − p ) , and the equation of the tangent line at a point ( r , s ) is y − s = − a 2 s b 2 r ( x − r ) . Now, if ( p , q ) and ( r , s ) have tangents that are perpendicular to each other, m 1 m 2 = − 1 , or ( − a 2 q b 2 p ) ( − a 2 s b 2 r ) = − 1 . Using this and the fact that ( r , s ) is on the ellipse so a 2 r 2 + b 2 s 2 = 1 gives r = ± b 6 p 2 + a 6 q 2 a 4 q and s = ∓ b 6 p 2 + a 6 q 2 b 4 p . Solving the two tangent line equations for x and y gives x = b 4 p 2 + a 4 q 2 ± a 2 q b 6 p 2 + a 6 q 2 + b 4 a 2 p and y = b 4 p 2 + a 4 q 2 ∓ b 2 p b 6 p 2 + a 6 q 2 + a 4 b 2 q , and x 2 + y 2 simplifies to a 2 + b 2 .