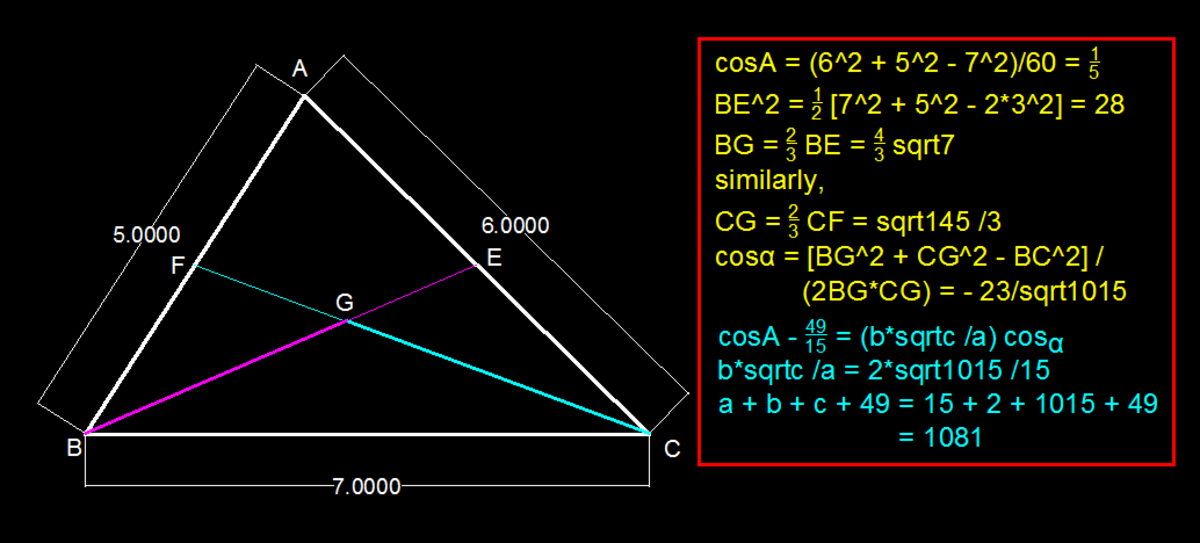
Angle Relationship

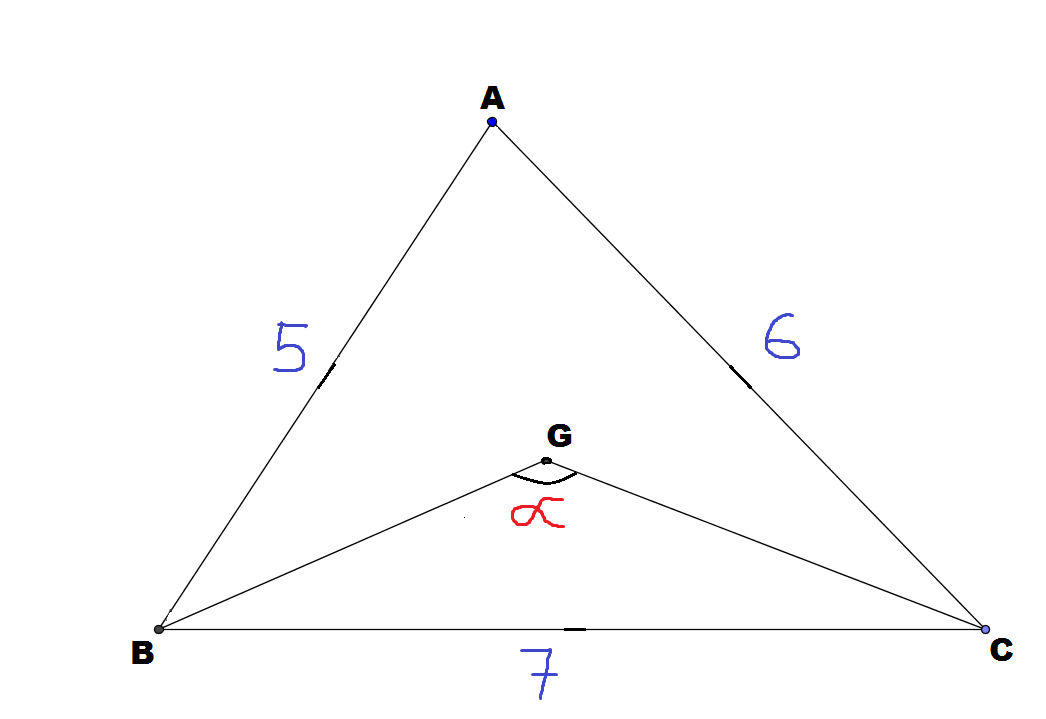
In the above image , $G$ is the centroid of $\Delta ABC$ and $AB=5 , AC=6 , BC=7$ .Let $m\angle BAC = A$ and $m\angle BGC=\alpha$ . If the relationship between the cosines of angles can be expressed as : $\cos A - \dfrac{49}{15} = \dfrac{\eta_2\sqrt{\eta_3}\cos\alpha}{\eta_1}$ where $\eta_{i}$ is a positive integer $\forall i \in \{1,2,3\}$ , $\eta_3$ is square free and $gcd(\eta_1,\eta_2)=1$

Find the value of $\eta_1 + \eta_2 + \eta_3 +49$ .

---

On the similar lines , we know:

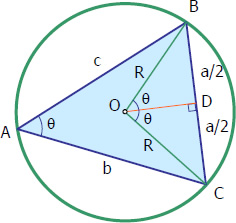
If you see the above image the angle subtended by side $BC$ on circumcenter $O$ is twice the measure of $\angle A$ subtended on circumference of the circumcircle.

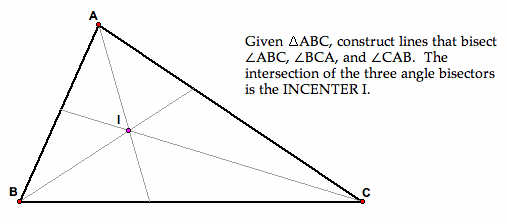
If you see the above image , if $I$ is the incenter , then the relationship between the angles subtended by $BC$ is $\angle BIC = 90^\circ + \dfrac{\angle A}{2}$ .

Having played with circumcenter and incenter , this problem is created to play with centroid. Hope you enjoy solving it.