Angle with tangent

Geometry Level 3

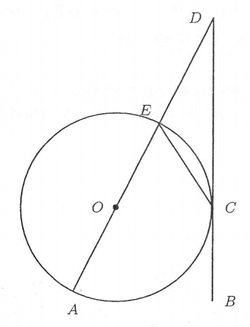In the figure above, the line $BD$ is tangent to the circle at $C$ . The line $AD$ passes through the centre $O$ of the circle and intersects the circle at $E$ .

It is given that $\angle CDE=34^{\circ}$ and $\angle DCE=x^{\circ}$ .

Find the value of $x$ .

This is a part of the Set .

The answer is 28.000.

4 solutions

A Former Brilliant Member
Sep 17, 2015

$\angle{OCD}=90\,^{\circ}$ So $\angle{DOC}=56\,^{\circ}$ Then we know that EOC is an isosceles triangle and $\angle{OEC}=\angle{ECO}=62\,^{\circ}$ Now $\angle{ECO}+x\,^{\circ}=90\,^{\circ}$ $x\,^{\circ}=90\,^{\circ}-62\,^{\circ}=28\,^{\circ}$

Hjalmar Orellana Soto
Sep 2, 2015

$\overline{OC}\perp \overline{BD} \rightarrow \angle COD = 54^{o}$ . As $\overline{OC}$ is radius, $\angle OEC = 62^{o}$ . So $x+34^{o}=62^{o} \rightarrow x=28^{o}$

Ano Maly
Aug 31, 2015

I put in 28, and it said the correct answer was 28.000. This has happened to more before on other problems. What should I do?

You got the points so just chill.

Kushagra Sahni - 5 years, 9 months ago

It's not actually about the points though :P

@Ano Maly I guess 28 is the same as 28.000 The problem setter set the problem in such a way maybe to confuse people. Some people won't try the answer as 28 after seeing "Decimals OK" It's fine, 28=28.000.

As @Kushagra Sahni said, Just chill.

Mehul Arora - 5 years, 9 months ago

Alan Yan
Aug 31, 2015

By Exterior Angle Theorem, $\angle CEA = x + 34$ .

Since $\angle CAE$ and $\angle ECD$ substend the same arc, they are congruent, implying that $\angle CAE = x$ .

Now construct segment $AC$ . Since $AE$ is a diameter, this implies that $\angle ECA = 90$ .

$\angle ECA , \angle CEA,$ and $\angle CAE$ are three angles of a triangle, which implies that

$\angle ECA + \angle CEA + \angle CAE = 180 \implies x + x + 34 = 90 \implies x = \boxed{28}$

Angle with tangent

This is a part of the Set .

The answer is 28.000.

4 solutions

0 pending reports