Supplementary Angles?
Given that D = 1 5 0 ∘ , Find the measure of the sum of angles A + B + C .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
why mess up with so much constructions ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
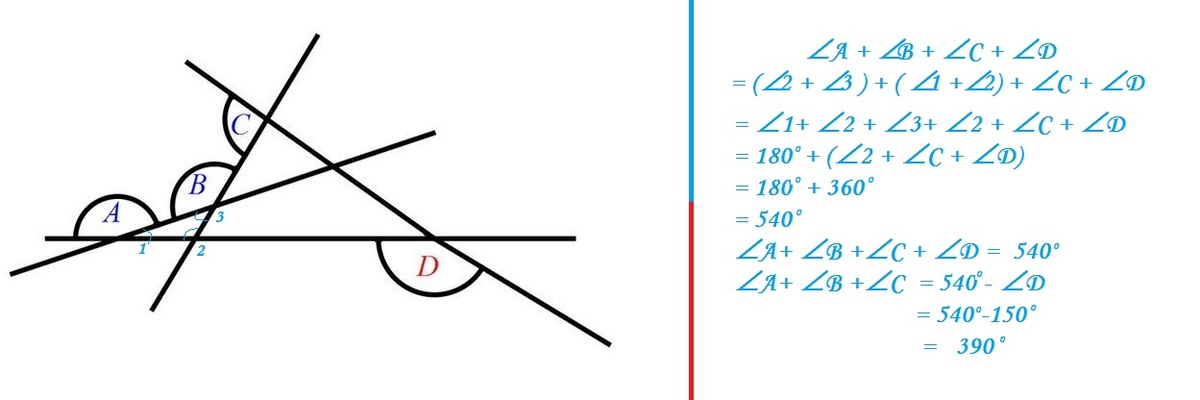 Properties used :::::::::
Properties used :::::::::
Exterior angle property of triangle
Sum of Exterior angles of a polygon = 360
Makes sense.
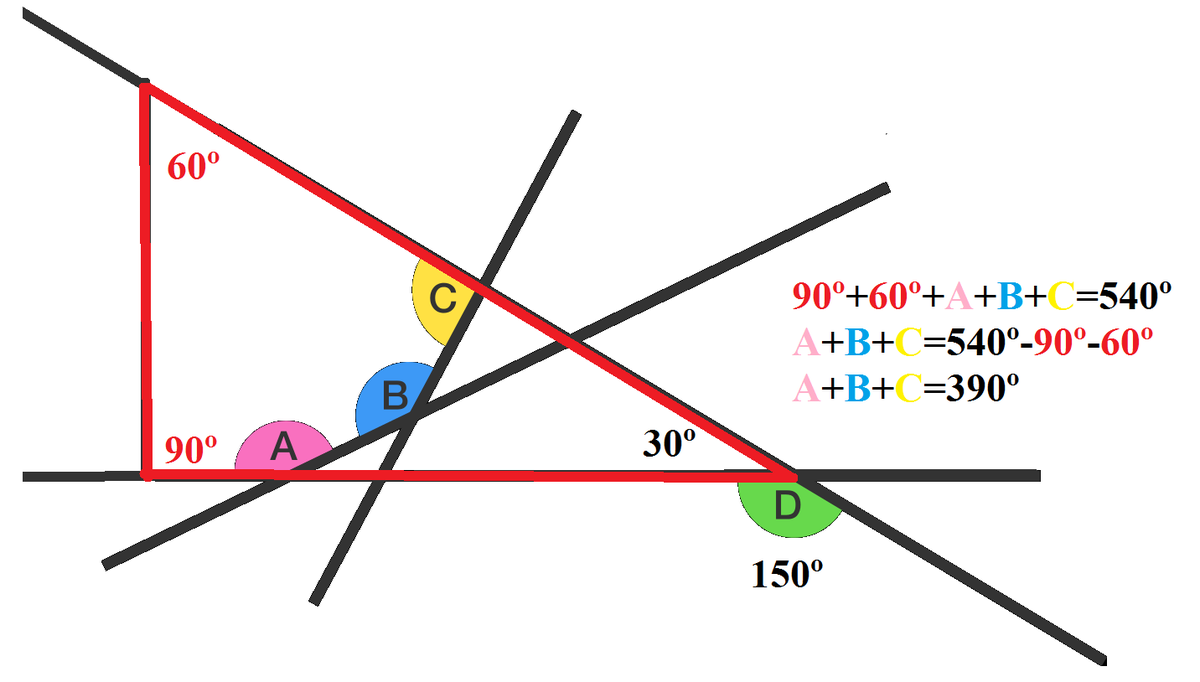
- I obtained the 30º triangle as 180º-150º.
- I used that angle to create the right triangle.
- We can see that those 90º and 60º angles were 2 of the internal angles of a pentagon.
- The sum of the internal angles of a pentagon is 540º, so we can substract 90º and 60º, and we get 390º.
There are two triangles in this question and one polygon. The complementary angle of "D" will be 30 degree. Label two other angles in the triangle as "M" and "N". so A = M + 30 (From the property of complementary angles) C = N + 30 (From the property of complementary angles) A + C - 60 = M + N
From the polygon in the middle we can have, N + B + M + 30 = 360 N + M + B = 330 A+C-60+B=330 A+B+C = 390
Great job.
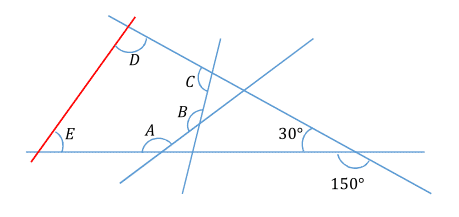 The
3
0
∘
-angle was obtained as
1
8
0
∘
−
1
5
0
∘
, and the red line has been added.
The
3
0
∘
-angle was obtained as
1
8
0
∘
−
1
5
0
∘
, and the red line has been added.
We see that D + E + 3 0 ∘ = 1 8 0 ∘ , since they are internal angles of the same a triangle. From that the sum D + E = 1 5 0 ∘ .
Angles A + B + C + D + E = 5 × 1 8 0 ∘ − 3 6 0 ∘ = 5 4 0 ∘ from the fact that they are internal angles of a pentagon.
All we need to do now is subtract the sum of D + E = 1 5 0 ∘ from this total to get the sum we need.
A + B + C = 5 4 0 ∘ − 1 5 0 ∘ = 3 9 0 ∘ .
I assumed C was a right angle. I also assumed that angle A and angle B were equal to D. It seems like it is a game of 30-60-90 triangles and 30-30-120 angles. I like the pentagon approach. The other seems too complicated when it looks obvious--is there a simpler more elegant path to the conclusion? I'm not really versed in this formula writing business.
Add a line E F so that
X + Y = 1 5 0
Based on the picture, the sum interior angles of 5 sides polygon = 5 4 0 ∘
A + B + C + X + Y = 5 4 0 ∘
A + B + C + 1 5 0 = 5 4 0 ∘
A + B + C = 3 9 0 ∘ .
Also, there is a second solution without adding lines:
Based on the picture, we know that,
A = Y + 3 0
B = Z
C = X + 3 0
As you can see, four of the angle form a quadrilateral, therefore,
A + B + C
= ( Y + 3 0 ) + ( Z ) + ( X + 3 0 )
= X + Y + Z + 6 0
= ( 3 3 0 ) + 6 0 ---------- ( Quadrilateral interior angle is 360, so 360 - 30 = 330 )
= 3 9 0 ∘