Angles
The figure below is made on the regular grid.
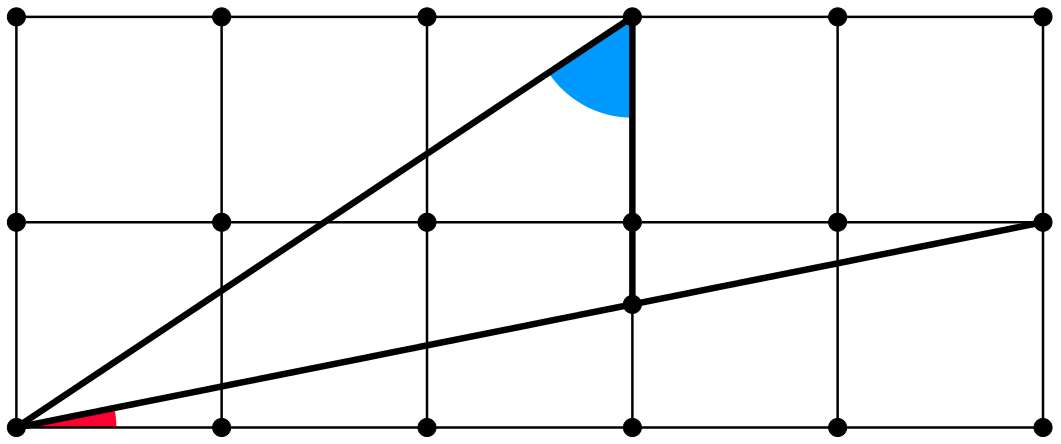
Find the value of blue angle − red angle .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I find it troublesome that the problem is given in a 2 by 6 matrix, the solution is given in a 3 by 6 matrix, the node C is not in the same place in the problem and solution. In the solution diagram the blue angle is clearly greater than 45 degrees.In the problem drawing, it seems that the blue angle is less than 45 degrees.Ed Gray
sin ( b l u e ) = 1 3 3
cos ( b l u e ) = 1 3 2
sin ( r e d ) = 2 6 1
cos ( r e d ) = 2 6 5
sin ( b l u e − r e d ) = 1 3 3 ⋅ 2 6 5 − 1 3 2 ⋅ 2 6 1 = 2 1 → b l u e − r e d = 4 5 o
△ A B C is isosceles, because A C = B C . In the other hand ∠ A C B = 9 0 ° , so ∠ B A C = ∠ C B A = 4 5 ° . (If you don't know why, just ask in comment, and I complete my solution.) Since ∠ D A C = blue angle , blue angle − red angle = 4 5 ° .