Solving A Pink Triangle
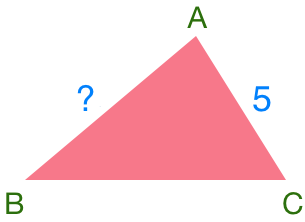
In Δ A B C , angle A is twice angle C , side B C is 2 units longer than side A B , and A C = 5 units. Find the length of A B .
The answer is 4.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Yes. Neat clean geometry. Only I wonder how you thought of it ! Up voted.
Nice one!Was your motivation the fact that an isosceles triangle having one angle π − 2 θ has the other two equal angles θ ?
Neat and tidy solution!!! I used the sine rule though.
Elegant solution
Using s i n e rule: sin A a = sin B b = sin C c ⇒ sin 2 C c + 2 = sin 3 C 5 = sin C c ( sin 2 C = 2 sin C cos C , sin 3 C = 3 sin C − 4 sin 3 C ) 2 cos C c + 2 = 3 − 4 sin 2 C 5 = 1 c From 1 and 3 find cos C while from 2 and 3 find sin 2 C in terms of c and use ( sin 2 C = 1 − cos 2 C ) . ⇒ 4 c 3 c − 5 = 1 − ( 2 c c + 2 ) 2 ⇒ c = 4 Hence A B = c = 4 .
Nice solution. I first used the sine rule to find that
c sin ( C ) = a sin ( 2 C ) ⟹ c sin ( C ) = c + 2 2 sin ( C ) cos ( C ) ⟹ cos ( C ) = 2 c c + 2 .
Then I used the cosine rule to find that
c 2 = 2 5 + ( c + 2 ) 2 − 1 0 ( c + 2 ) cos ( C ) ⟹ cos ( C ) = 1 0 ( c + 2 ) 4 c + 2 9 .
Equating these two expressions for cos ( C ) then gives us that
2 c c + 2 = 1 0 ( c + 2 ) 4 c + 2 9 ⟹ 5 ( c + 2 ) 2 = c ( 4 c + 2 9 )
⟹ c 2 − 9 c + 2 0 = ( c − 4 ) ( c − 5 ) = 0 ,
and so either c = 4 or c = 5 . We can confirm that the first value satisfies the requirements of the question but the second value does not, (although it comes very close to doing so). I find it curious why the c = 5 value, while extraneous, shows up at all.
Having said all this, I do find Maria's solution to be the most elegant approach.
Log in to reply
Same method sir!If c=5 then the smaller angle would become 45° but then there would be a right angle and that is not satisfied by (5,5,7).
Log in to reply
Exactly Same Interpretation.
Yes, the smaller angle would be close to 4 5 ∘ , but not exactly. The angles in a 5 / 5 / 7 triangle are ( 4 5 . 5 7 3 ∘ , 4 5 . 5 7 3 ∘ , 8 8 . 8 5 4 ∘ ) , which means that angle A is not twice angle C . I was just surprised that c = 5 popped out as a potential solution even though it ends up not actually satisfying the given requirements. I don't normally give much thought to why extraneous solutions occur, but I did find this one a bit unusual.
Exactly Same Way.
Same Sin and Cos Laws. With c=5, an isosceles triangle, A should be 90. Though near it was not 90 as pointed out by Adarsh Kumar.
Did the same ! Upvoted
Can you think of a synthetic approach also ?
Log in to reply
And what's that? Can you give a hint (or an example)??
Log in to reply
It means using only Euclidean methods ( like similarity, congruence and auxiliary constructions ) to come to the solution.
Here is another solution, this time using Euclidean methods only. Let bisector of ∠ A intersect B C at D . A D = D C and △ A B C similar to △ D B A . To simplify notation let A D = x , A B = y . x 5 = y y + 2 = y + 2 − x y This gives values of x = 1 0 / 3 , y = 4
Nice one :)
Same way! Easy overrated question
I did a straightforward solution.
Let ∠ C = θ , then ∠ A = 2 θ and ∠ B = 1 8 0 ∘ − 3 θ . Let A B = x , then B C = x + 2 .
Using sine rule, we have:
⎩ ⎪ ⎨ ⎪ ⎧ x + 2 sin ( 2 θ ) = x sin θ 5 sin ( 1 8 0 ∘ − 3 θ ) = x sin θ . . . ( 1 ) . . . ( 2 )
( 1 ) : x sin ( 2 θ ) 2 x sin θ cos θ 2 x cos θ = ( x + 2 ) sin θ = ( x + 2 ) sin θ = x + 2
( 2 ) : x sin ( 1 8 0 ∘ − 3 θ ) x sin ( 3 θ ) x ( sin θ cos ( 2 θ ) + cos θ sin ( 2 θ ) ) x ( cos ( 2 θ ) + 2 cos 2 θ ) x ( 2 cos 2 θ − 1 + 2 cos 2 θ ) 4 x cos 2 θ − x x ( 2 x cos θ ) 2 − x x ( x + 2 ) 2 − x x 2 + 4 x + 4 − x 2 ⇒ x = 5 sin θ = 5 sin θ = 5 sin θ = 5 = 5 = 5 = 5 = 5 = 5 x = 4
Yeah, trig bash is indeed straightforward, sir. Even I solved the problem in a similar way, but I guess everyone has to agree that Euclidean solutions are more elementary and aesthetically pleasing :). Btw upvoted !
AN EASY OVER RATED PROBLEM AGAIN!!!!!!!!!!!!!

1 . Extend A B to a point D such that A C = A D . Join C D .
2 . Now notice that △ A B C similar to △ C B D .
3 . Set ∣ A B ∣ = a and therefore ∣ B C ∣ = a + 2 .
4 . a + 2 a = a + 5 a + 2 because of the similarity.
This gives the solution ∣ A B ∣ = a = 4 .