Angles in a Acute Triangle
In acute triangle △ A B C , ∠ C A B = 3 4 ∘ and E is the foot of the perpendicular from B to A C . A point H on line segment B E is chosen, and X is the foot of the perpendicular from H to A B . What is the measure (in degrees) of ∠ E H X ?
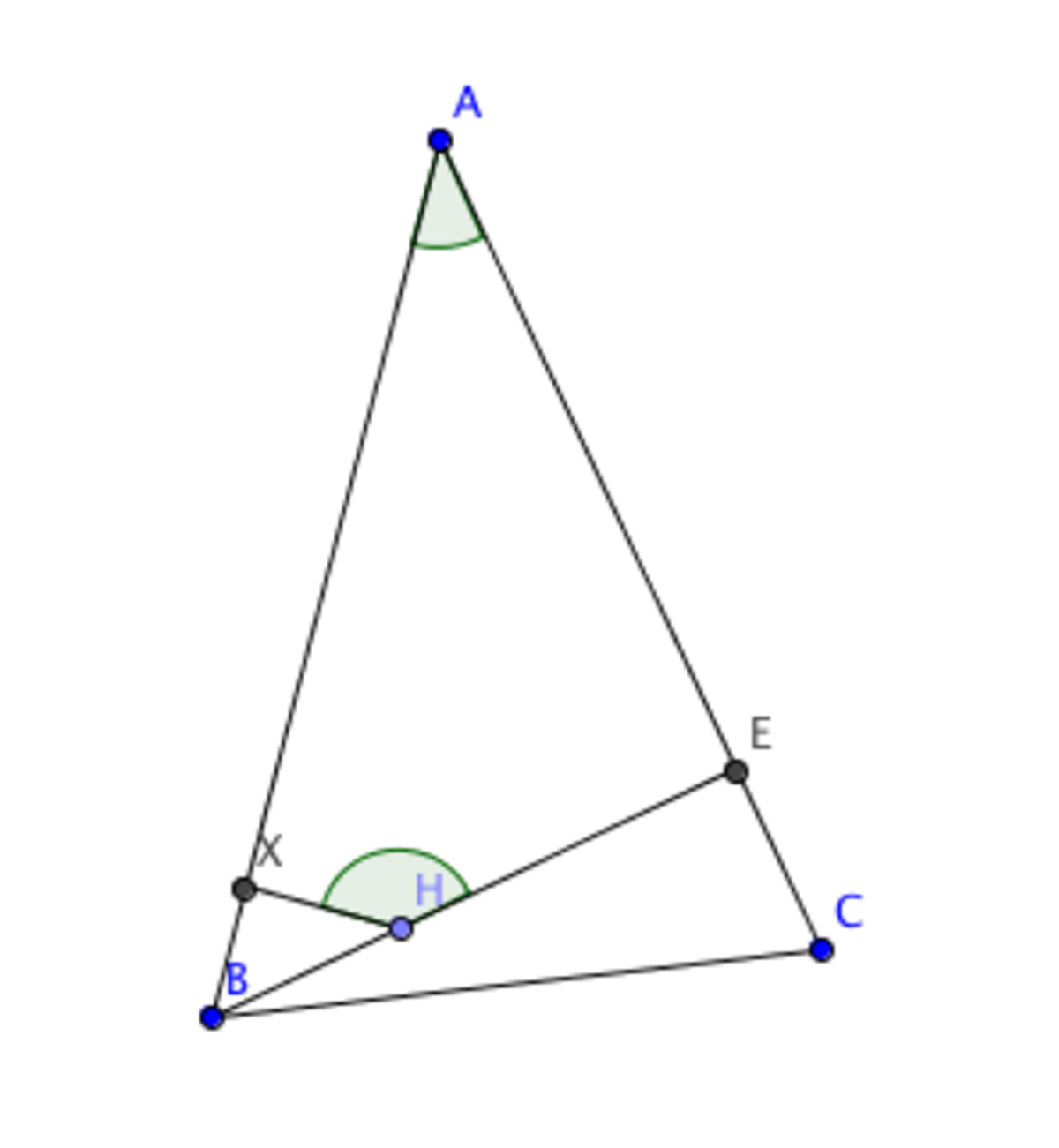
The answer is 146.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
Nice observation that A E H X is a cyclic quadrilateral.
Consider the quadrilateral AEHX, we know that sum of all the interior angles of a quadrilateral is 360degrees. It is given that E, and X are the perpendiculars, also given that ∠CAB=34degrees. So, ∠EHX=360-[90+90+34] = 146degrees.
XHEA is a quadrilateral and it's given that HX is perpendicular to AB and forms a 90 deg angle, and same goes with HE to AC. Angle A is 34 deg.
The sum of the interior angles of a quadrilateral is 360 deg angle AXH + angle XHE + angle HEA + angle A = 360
90 + angle XHE + 90 + 34 = 360
giving us angle XHE = 146
∠CAB=34°, ∠AEB=90° beacuse line EB is perpendicular to line AC, ∠AXH=90° because line XH is perpendicular to line AB
Supposed, ∠CAB=a ∠AEB=b ∠AXH=c & ∠EHX=d
a+b+c+d=360°
34°+90°+90°+d=360°
d=360°-214°
d=146°
sum of angle of an rectangle is 360 degree, so, angle EHX = 360 - (90 + 90 + 34) = 146
(Angles ABC and ACB are not needed to answer this question) The sum of angles in a Quadrilateral AXHE= 360 degrees. AXHE is a Quadrilateral. Line BE is a perpendicular line so angle AEH=90. Line HX is also a perpendicular so angle AXH is also 90 degrees. Therefore, angle EHX =360-(34+90+90)= 146 degrees.
Moderator note:
Good observation that the answer is independent of the values of angles A B C and A C B .
E B A = 9 0 o − 3 4 o = 5 6 o ;
X H B = 9 0 o − 5 6 o = 3 4 o
E H X = 1 8 0 o − 3 4 o = 1 4 6 o
Since angle AXH = angle AEH = 90 degree, we can conclude that AEHX are vertices of a cyclic quadrilateral.
Hence, since the opposite angles of a cyclic quadrilateral are supplementary, angle EHX = 146 degree