Angles Sum

Geometry Level 2

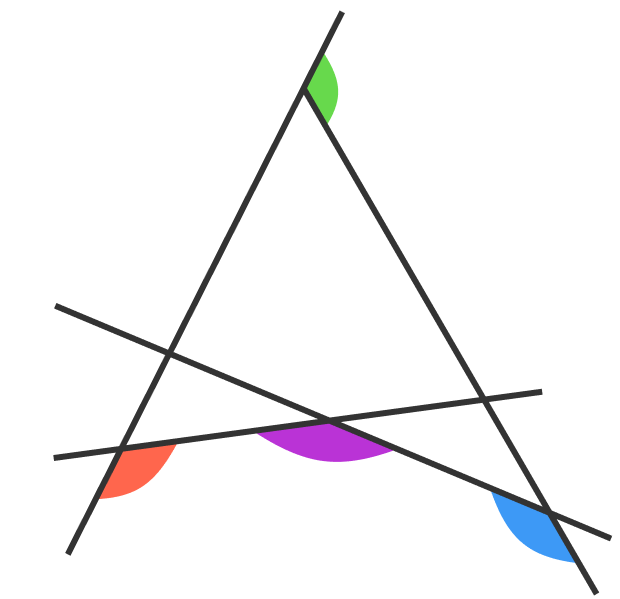
Find the sum (in degrees) of the four colored angles in the diagram.

360 480 540 600

View wiki
Leah Smith by Leah Smith , 25, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

Eli Ross Staff
Sep 16, 2015

There are quite a few nice approaches to this problem! Here's one of them, but can you find any others?

51 Helpful 2 Interesting 4 Brilliant 0 Confused

There is a nice trick using a pencil, rotating the pencil every time we come across an angle. The final rotation of the pencil after going through all the angles is 54 0 ∘ 540^{\circ} which is our answer.

Daniel Liu - 5 years, 9 months ago

Very nicely done

Von S - 4 years, 7 months ago

Pretty neat. Congratulations

Omar Monteagudo - 4 years ago

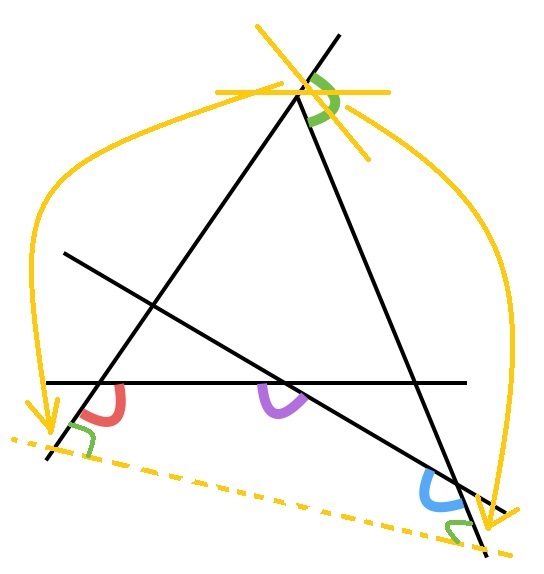after drawing the orange line you make a big triangle and five sides polygons the green angle can be converted to the opposite triangle interior angles to be the left two angles of the polygons.

the interior angles of the five sides polygons is 180(5-2) = 540

29 Helpful 0 Interesting 3 Brilliant 0 Confused

Very nice solution!

Alex Bean - 4 years, 10 months ago

Wow! Such an indirect and elegant solution. Very nice imagination!

Muneeb Aadil - 4 years, 4 months ago
Mahade Hasan
Sep 16, 2015

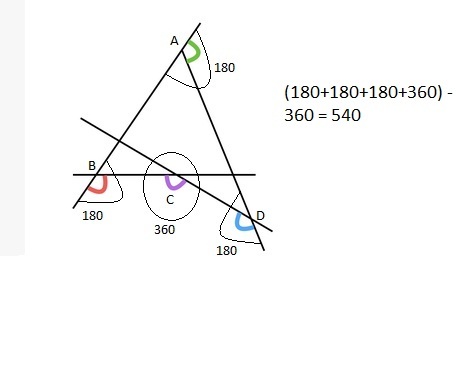
As ABCD is a quadrilateral.. then the sum of all(4) interior angles is (n - 2) 180=>(4 - 2) 180=360. Now the sum of GREEN, RED and BLUE angles and their supplementary angles is 180+180+180 and sum of VIOLET angle and its explementary angle is 360. Now (180+180+180+360) - 360{(4 - 2)*360)} = 540

9 Helpful 0 Interesting 0 Brilliant 0 Confused

ABCD is a quadrilateral not a rectangle.

Hrituparna Mandal - 5 years, 9 months ago

Log in to reply

yes.. sorry... updating

Mahade Hasan - 5 years, 9 months ago
Shubham Java
Sep 18, 2015

Easiest method!!!

I have marked 2 more angles than shown in the question...

Sum of the angles of a triangle is 180°. ∴sum of exterior angles 1,2 and 6 is 360°

∴ ∠1+∠2+∠6=360° ...... 1

Similarily

∠4+∠5+∠3=360° ...... 2

∠3=180°-∠6 Using this in 2:

∠4+∠5+(180°-∠6)=360° .......3

Now adding 1 and 3 we get ∠1+∠2+∠6+∠4+∠5+(180°-∠6)=720°

⇒ ∠1+∠2+∠4+∠5+180°=720°

⇒ ∠1+∠2+∠4+∠5=540°

3 Helpful 0 Interesting 0 Brilliant 0 Confused

I don´t think the method I used is right in every case, but it was in this one. We know that every angle is greater than 90 but less than 180. So I multiplied 90 times 4 and 180 times 4. Then I summed the two results and divided by two.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...