Angling all the way...
Triangle ABC has AC = BC , angle ACB = 96 , D is a point in ABC such that angle DAB = 18 and angle DBA = 30 . What is the measure of angle ACD .
All the angles are in Degrees.
To try more such problems click here .
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Up voted. Very good out of box approach. I solved by common path, Sin Law.
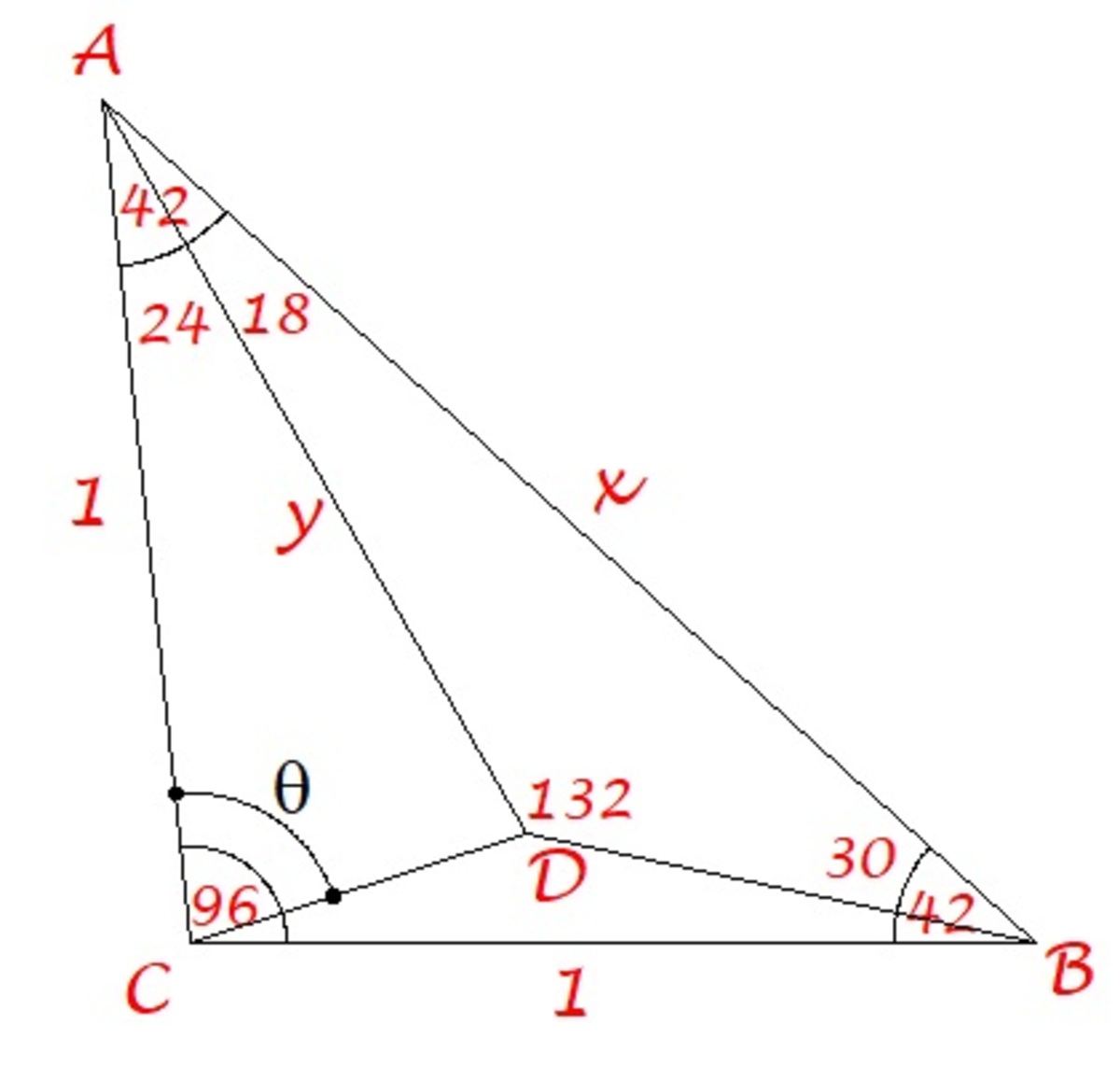
Let A C = B C = 1 .
By law of cosines, we have
x 2 = 1 2 + 1 2 − 2 ( 1 ) ( 1 ) ( cos 9 6 ) ⟹ x = 1 . 4 8 6 3
By law of sines, we have
sin 3 0 y = sin 1 3 2 1 . 4 8 6 3 ⟹ y = 1
Therefore △ C A D is isosceles with A C = A D = 1 . So
θ = 2 1 8 0 − 2 4 = 7 8
Good way of thinking.
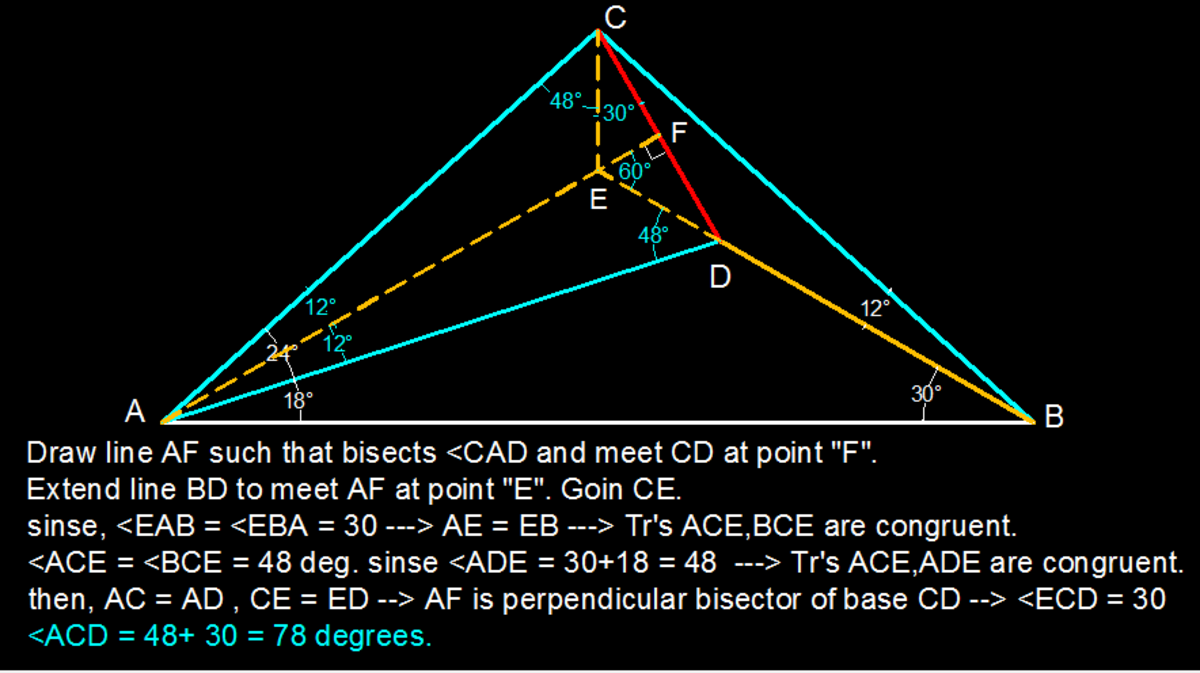
After constructing the figure as said, I tried joining C to the midpoint of AB, lets call it M. Now, AM = AB/2 = ACsin(half of Angle C) = ACsin48 Also, using sine rule, AD/sin30 = AB/sin132 = AB/sin48 Therefore, AD = AC, giving us ACD = 78 degrees.