Anisotropic Resistivity
 A material has anisotropic resistivity such that its resistivity in one direction say along the x axis has maximum value
and minimum value
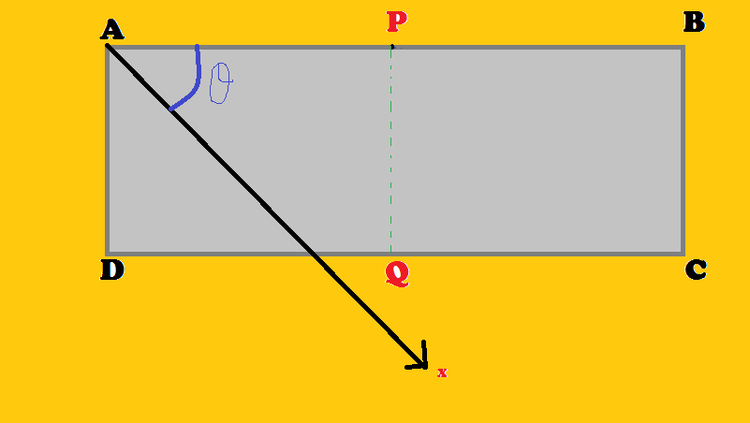
along other axes which are perpendicular to the x-axis from a specimen of such a material is cut a strip ABCD of length l=9cm and width b=1cm . The x-axis passes through the strip making an angle
with the edge AB as shown in the figure. If between the faces AD and BC a constant potential 196 is applied. The potential difference between points P and Q of the midpoints of AB and CD respectively that you will expect is maximum when
A material has anisotropic resistivity such that its resistivity in one direction say along the x axis has maximum value
and minimum value
along other axes which are perpendicular to the x-axis from a specimen of such a material is cut a strip ABCD of length l=9cm and width b=1cm . The x-axis passes through the strip making an angle
with the edge AB as shown in the figure. If between the faces AD and BC a constant potential 196 is applied. The potential difference between points P and Q of the midpoints of AB and CD respectively that you will expect is maximum when
find where [.] Is greatest integer function
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!