Another Artificial Capacitor
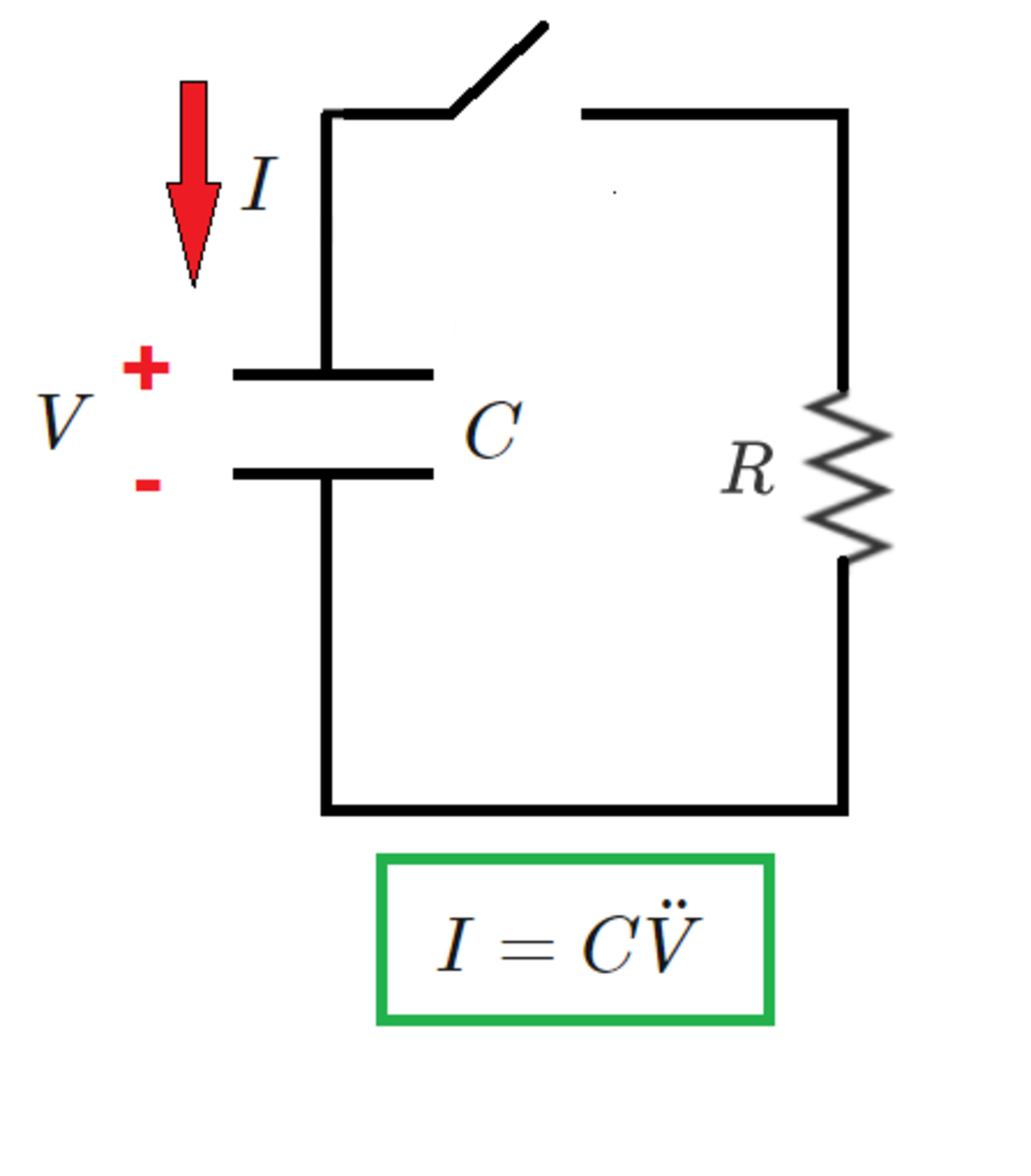
Suppose we had an artificial capacitor whose current was proportional to the second time-derivative of its voltage, as shown in the circuit diagram.
The switch closes at time . At this time, the capacitor voltage and its derivative are:
This artificial capacitor is an active element, with a battery as an internal energy source (not shown in the diagram).
Let the voltage signal period be . How much energy must the battery supply to keep the circuit operational from to ?
Note: Observe the sign conventions shown in the diagram
Details:
1)
2)
The answer is 2693.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Looking at the circuit, its equation can be written using Kirchoff's voltage law as follows:
V + I R = 0 ⟹ V + R C V ¨ = 0
Given that R = 2 and C = 3 , the equation can be rewritten as:
V ¨ + 6 1 V = 0
The general solution is:
V = A cos ( 6 t ) + B sin ( 6 t )
Plugging in the initial conditions and solving for A and B gives:
V = 1 0 ( cos ( 6 t ) + 6 sin ( 6 t ) )
Also,
I = C V ¨ ⟹ I = − 2 V
The period of the circuit is:
T = 2 π 6
Consider the circuit equation:
V + I R = 0
Multiplying the equation with I d t gives:
V I d t + I 2 R d t = 0 ⟹ ∫ 0 T I 2 R d t = ∫ 0 T − V I d t
This equation can be interpreted as: 'The energy dissipated by the resistor is equal to the energy supplied to the circuit'. From here, the energy supplied by the active element is concluded to be:
E = − ∫ 0 T V I d t = − ∫ 0 T V ( 2 − V ) d t = 2 1 ∫ 0 T V 2 d t
E = 5 0 ∫ 0 T ( cos ( 6 t ) + 6 sin ( 6 t ) ) 2 d t Solving this integral gives:
E = 3 5 0 π 6 = 2 6 9 3 . 3 5
This is indeed quite interesting. If one looks at a plot of voltage vs. time, it can be seen that the capacitor periodically charges (The voltage across it increases). This is contrary to conventional understanding that a charged capacitor when attached to a resistor only discharges.