Another covering problem
This star has five spokes that are each 1 unit long, and the angles between adjacent spokes are all the same.
How many copies of this star would you need to completely cover a bigger star with spokes of length 1 . 1 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Your problem from last week has inspired quite a few of us.
What a mathematician guy with your lingo and rigorousness ;).
Log in to reply
Hahahaha... Yup! Perhaps now that it's a featured problem I should spruce it up a bit... 😎
But the question asked for the number of copies of this star, not the total number of stars. I went with 1 original and 5 copies.
Log in to reply
5 copies aren't enough to cover the middle and the end of each spoke.
Log in to reply
You Con would like to use 6. The original plus 5 copies.
Yeah wirh 5 copies you then have 6 stars in total
I say it depends on the width of each spoke. if the width is = .1 u, you can do it with fewer.
Log in to reply
Interesting... Can you show a picture?
No yo uqould still need 4. 1 on the center. 2 covering 2 spokes each with the cover starts being sideways just to cover the end apokea. 1 to cover the remaining spoke.
Log in to reply
Hm, can you add a picture drawn to scale? I don't think that is truly possible. I get that you want to cover 2 of the tips with the star, but I don't think the tips would be covered perfectly.
One scaled up copy would do the trick ;)
I supposed a different definition of "cover." That is, a cover need only span the convex area. That lead me to say 3, as in the inspiration.
Log in to reply
Interesting perspective. Then it becomes this problem.
I had the same intuition. The text is misleading, what does "cover" really means ??
The problem should specify that the spokes thickness is 0, and that the picture is misleading, because if the thickness is 0.1 on more u can do it with 4 stars as someone already said. I copyed the pictures to test my idea and using that picture I was able to cover the extended version with 4 stars
Log in to reply
I agree that the thickness should be specified. I would be interesting to see the pictures. Where did you say you posted them?
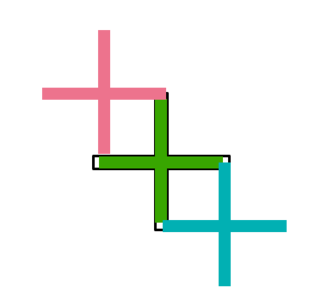
Hm, can you add a picture drawn to scale? I don't think that is truly possible. I get that you want to cover 2 of the tips with the star, but I don't think the tips would be covered perfectly.
Taking the simpler example where we have a star with 4 spokes which form right angles that line up nicely, you can see that the additional width isn't enough to help us cover 2 spokes, precisely because the length from the tip to the center is only 1.0, and so it cannot reach the 1.1 that is needed.
Please clarify if I interpreted your statement incorrectly. It might be possible that you do something creative with the angling of the width that allows us to cover the tips using the width, and if so, I would appreciate further clarification.
Edit: A possible interpretation is that the larger star with side length 1.1 has
no width
, while the smaller star with side length 1 has a width of 0.1. In this case, then yes we can use the additional width to make up for the additional length, since we do not need to also reach further due to the width of the large star. However, I don't think it's fair that the width doesn't apply to the larger star.
Also, in this case, I am concerned that the angles of the 5 pointed star might not allow the fattened star to reach the tips, though of course if we had a width of say 0.5, that could be possible. I have not done the calculations in this case.
Lies are not good here.
Not so scientific but justifiably correct and also not boring.
this problem is a non sense, and terribly set and explained.
Every star can cover only 1 line (intersections are 0d (points) and hence do not count as coverage ad they have no length) unless the star is at the centre. All stars can also not cover the whole of the line they cover, there are 5 lines to cover, so the answer must be over 6. You can find a 6 solution through using a star to cover the end of each line (5 stars used) and an additional star in the middle. 1+1=2>1.1 so this will cover the all of the line for each line.
Excellent sir.
You can cover six by putting one in the center, and five on each of the end bits.
And you can't do any better since, the only way to cover more than one line is to go in the center, and once you've done that, you need to cover each of the end bits with a separate five spoked shape thingy...