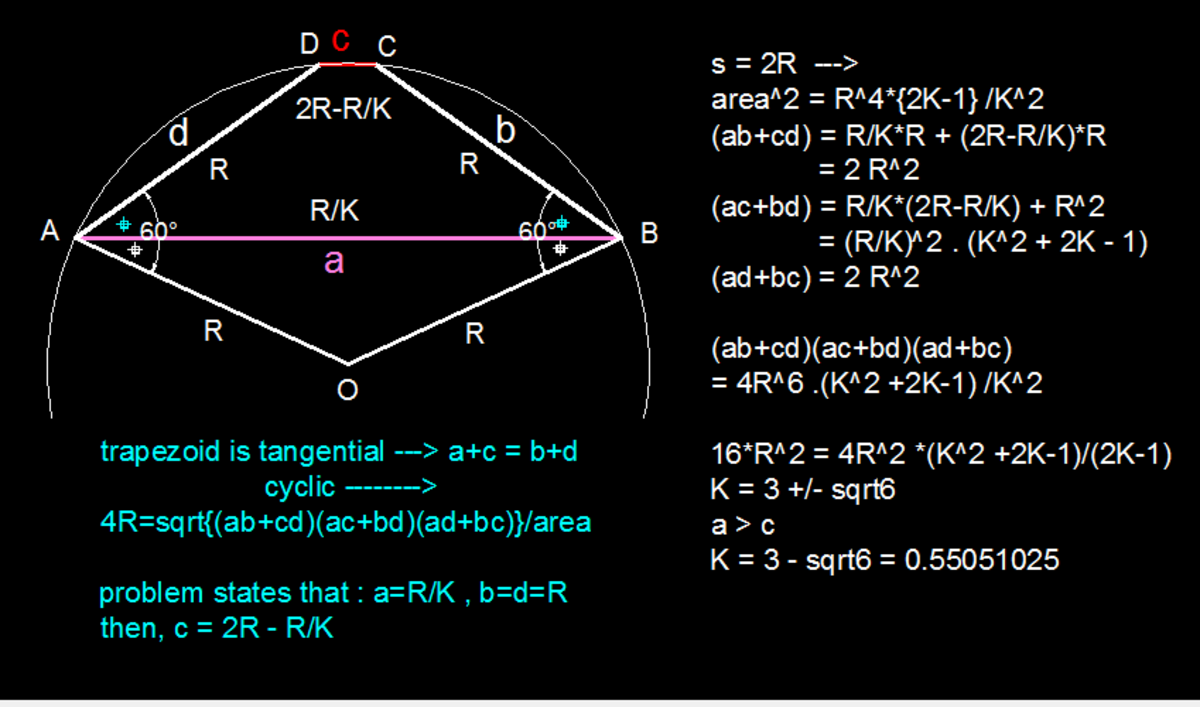
Another Cyclic Trapezoid

Call the center of the larger circle $Z$ and call the smaller circle $X$ . Furthermore, let $E, F, G, H$ be the points on $AB, BC, CD, AD$ , respectively, where circle $X$ is tangent. We know that $GC=FC$ and $EB=FB$ . Furthermore, by symmetry, we see that $E$ is the midpoint of $AB$ and $G$ is the midpoint of $CD$ . If we say $AB=b$ and $CD=a$ , then we have $R=BC=BF+CF=\frac{a}{2}+\frac{b}{2}$ , so $a+b=2R$ , and the semi-perimeter can be expressed as $S=\frac{R+R+a+b}{2}=\frac{R+R+(2R)}{2}=2R$ .

Next, we calculate the area of $ABCD$ : $A=\sqrt{(S-a)(S-R)(S-b)(S-R)}=R\sqrt{(2R-a)(2R-b)}=R\sqrt{ab}$ . Using the area of a trapezoid formula,

$R\sqrt{ab}=A=h\frac{b_1+b_2}{2}$

$R\sqrt{ab}=(EZ+GZ)\frac{a+b}{2}$

$R\sqrt{ab}=\big( \sqrt{BZ^2-BE^2}+\sqrt{CZ^2-CG^2}\big) \cdot R$

$\sqrt{ab}=\sqrt{R^2-\big( \frac{a}{2}\big) ^2}+\sqrt{R^2-\big( \frac{b}{2}\big) ^2}$

$ab=\big( R^2-\big( \frac{a}{2}\big) ^2\big) +2\sqrt{\big( R^2-\big(\frac{a}{2}\big) ^2\big) \big( R^2-\big( \frac{b}{2}\big) ^2\big) }+\big( R^2-\big( \frac{b}{2}\big) ^2\big)$

$\frac{(a+b)^2}{4}+\frac{ab}{2}-2R^2=2\sqrt{\big( R^2-\big( \frac{a}{2}\big) ^2\big) \big( R^2-\big( \frac{b}{2}\big) ^2\big) }$

$ab-2R^2=\sqrt{(4R^2-a^2)(4R^2-b^2)}$

$a^2b^2-4R^2ab+4R^4=16R^4-4(a^2+b^2)R^2+a^2b^2$

$4(a^2+2ab+b^2-3ab)R^2=12R^4$

$4R^2-3ab=3R^2$

$R^2=3ab=3b(2R-b)$

$R^2-6bR+3b^2=0$ .

And using the quadratic formula, we get $R=(3\pm \sqrt{6})b$ . Using these values to solve for $a$ , we get $R=(3\mp \sqrt{6})a$ . Since we know that $b>a$ , we take the larger value of $b$ as the only valid solution. Thus $\boxed{R=(3-\sqrt{6})b}$ is the valid solution.