Another Pi, wanna have some pie?
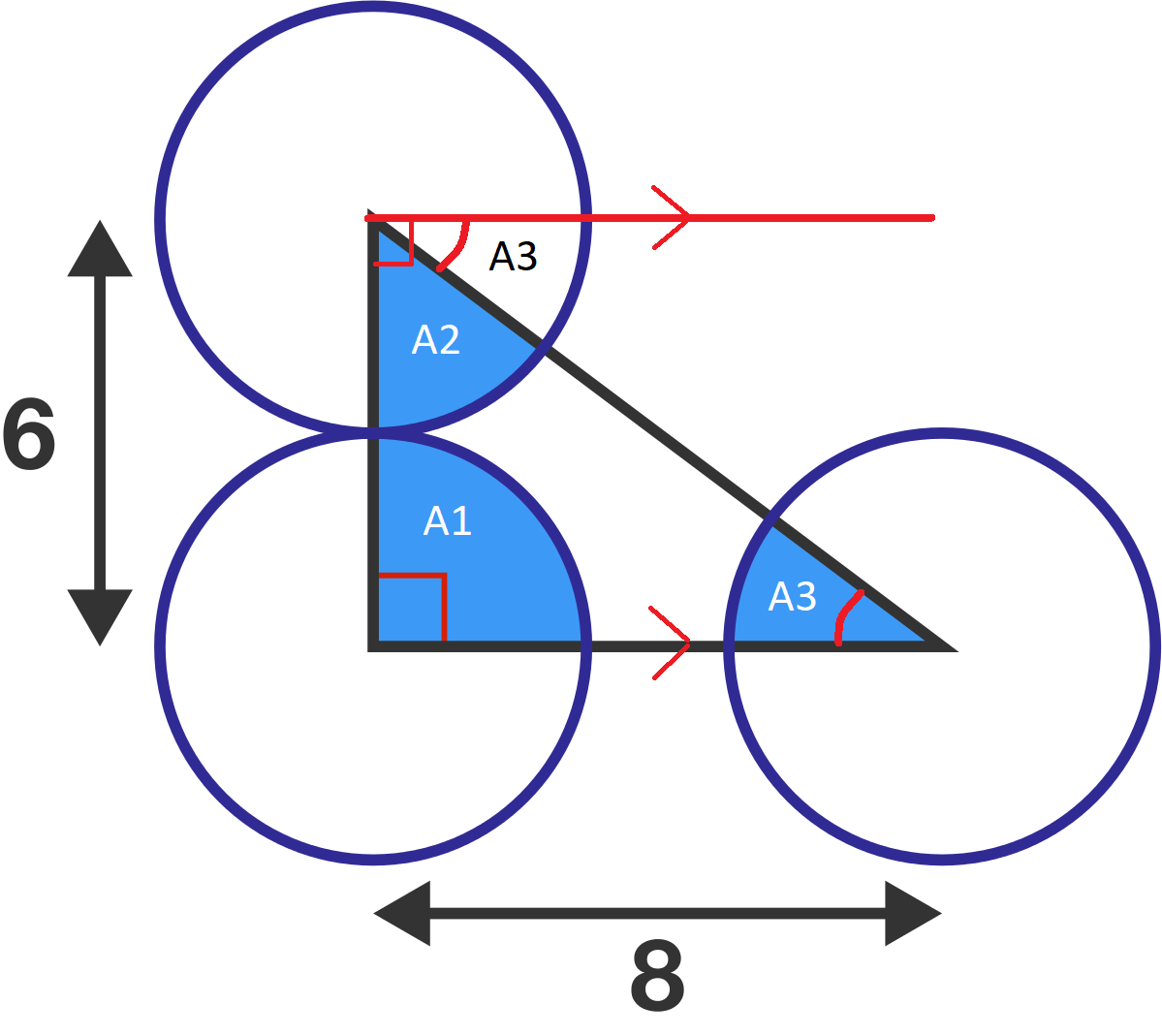
The three circles are identical and centered on the triangle's vertices. Two of the circles are tangent to each other.
What is the blue area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Nice solution
Damn, I forgot it was supposed to be ½πr^2 and not just ½πr so I just guessed the answer haha
Simple and perfect explanation!
idk what or how to solve these complex equasions i do not under stand because i am 10
Hey! Can you explain the final simplification? I'm pretty rusty on that part. Thank you!
Log in to reply
The area of a circle is π r 2 , so the area of half a circle is 2 1 π r 2 . Since the radius is 3 , replace r with 3 to get 2 1 π 3 2 . This simplifies to 2 1 π 9 = 2 1 1 π 1 9 = 2 9 π .
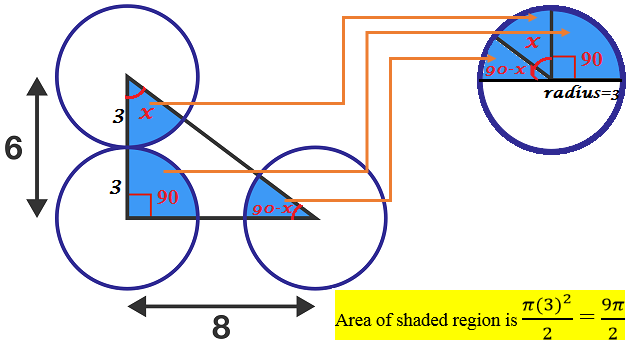 The sum of the angles in a triangle is 180 degrees. In the given triangle, one of the angle is 90 degrees and remaining two unknown angles are 'x' & '90-x' degrees respectively. The radius of the circle is
2
6
= 3.(circles are tangent to each with length of 6)
The sum of the angles in a triangle is 180 degrees. In the given triangle, one of the angle is 90 degrees and remaining two unknown angles are 'x' & '90-x' degrees respectively. The radius of the circle is
2
6
= 3.(circles are tangent to each with length of 6)
The imaginary circle on the right constructed with the radius of 3 & the sectors of blue shaded region of the left side image.(sum of angles of the sectors equal to 180 degrees)
Sir can I know how you create these type of pictures. I want to learn because it will be helpful in editing my questions.
The radius of the circle(s) is 2 6 = 3 ,combine the dark areas and get a semicircle. 3 2 π × 2 1 = 4 . 5 π
 The sum of the interior angles of a triangle is 180 degrees. Since the three circles are identical (each has a radius of 3), the area of the blue region is equal to the area of a semi-circle of radius 3. So the desired area is
The sum of the interior angles of a triangle is 180 degrees. Since the three circles are identical (each has a radius of 3), the area of the blue region is equal to the area of a semi-circle of radius 3. So the desired area is
A = 2 1 π r 2 = 2 1 π ( 3 2 ) = 2 9 π
Marvin how will you edit and create these pictures.
None of the answer are correct. Area is a squared term...
We need to know that there are 180 degrees in a triangle. From there we can deduce that the three shaded regions make up half (180 degrees) of a circle, and since the regions are all sectors from the same sized circle, we know the radius of the combined half circle is the radius of the three pictured circles. This radius is 3 from the picture. The are of the shaded regions is therefore 1/2 of the area of a circle with radius 3, or 9pi/2.
If you add the segment on the right to the segment on the top-left, you would get the segment on the bottom right. This can be shown by considering what would happen if you stretched out the bottom length to infinity. Together, these two segments add to half a circle which is answer B: 9 p i /2.
The radius of the tangent circles is 3. The area of a circle is pi * r^2. The angles of a triangle always add up to 180. Therefore, the angles of a triangle will give you half a circle since the angle of a circle is 360. Plugging in the numbers for the formula for 1/2 the area of a circle (1/2 pi * r^2), gives you 1/2 pi * 3^2. Simplify gives you pi * 9 / 2.
The three blue areas form three sectors are also the three angles in the triangle. As the circles are identical the total area of a sector which subtends 180 degrees is nothing but pi * r * r /2 which evaluates to 9*pi /4.
If we construct a red horizontal line which is parallel to the base of the right-angled triangle, we can treat the hypotenuse as a transversal line. The angle in the bottom right of the triangle corresponds to the angle between the hypotenuse and the red parallel line.
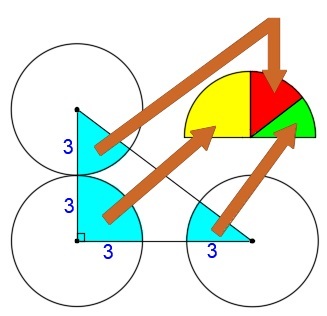
Since the circles are identical, area A 3 is the same for both sectors. We can see then that A 1 = A 2 + A 3 .
The shaded area is therefore A S = 2 A 1 , or two quarters of a circle (or half a circle).
If we look at the bottom left circle, the radius is simply half the distance between the centres of the two circles (they are touching!), so r = 3 .
The area of a circle is A = π r 2 , so the solution is therefore A S = 2 1 π r 2 = 2 π × 3 2 = 2 9 π
Best explanation
liked this one the most
area of a one circle is 9pi,then total area blue coloured region in all circles =(9π÷4)+2(9π÷8)=(9π÷2)
Since the circles are identical and the distance between the centres of the tangential ones is 6, each circle has radius 3.
Now, by letting the internal angles of the triangle be θ 1 , θ 2 , θ 3 (measured in radians), and using the formula: Sector Area = 2 θ ⋅ r 2 , we get,
Total blue area = Sum of individual areas Total blue area = 2 θ 1 ⋅ r 2 + 2 θ 2 ⋅ r 2 + 2 θ 3 ⋅ r 2 Total blue area = ( θ 1 + θ 2 + θ 3 ) ⋅ 2 r 2
Since the sum of the angles in a triangle is π radians (meaning that combining the areas makes a semicircle), Total blue area = π ⋅ 2 3 2 = 2 9 π
Since two of the circles are tangent to each other on the side of the triangle that is 6 , the radius of each circle is r = 2 6 = 3 .
Since the angles of a triangle add up to 1 8 0 ° , all the blue sectors have a combined central angle of 1 8 0 ° , or half a circle.
Therefore, the total blue area is equivalent to the area of half a circle with a radius of 3 , which is A = 2 1 π 3 2 = 2 9 π .