Another Pi
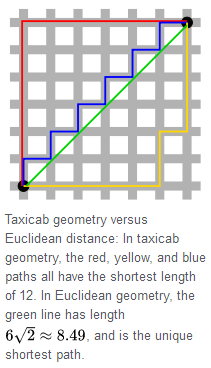
In taxicab geometry, Euclidean distance for a point ( x 1 , y 1 ) and a point ( x 2 , y 2 ) d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 is replaced by Manhattan distance d = ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ and the shape of circles may change as well.
What is the value of Pi, defined as the ratio of a circle's circumference to its diameter, in taxicab geometry?
The answer is 4.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Alternatively, the formula of arc length in Euclidean geometry s = ∫ a b 1 + ( d x d y ) 2 d x is replaced by s = ∫ a b ( 1 + ∣ ∣ ∣ ∣ d x d y ∣ ∣ ∣ ∣ ) d x in taxicab geometry. In this case, the length of side is given by l = ∫ 0 r ( 1 + ∣ ∣ ∣ ∣ d x d ( r − x ) ∣ ∣ ∣ ∣ ) d x = 2 ∫ 0 r d x = 2 r .