Another Pointy Quadrilateral
What is the area of quadrilateral E F G H ?
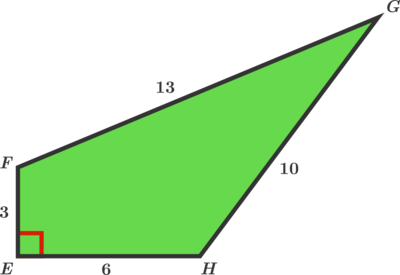
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
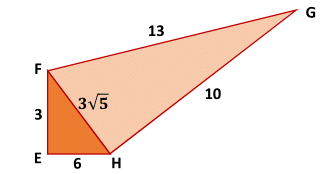 The hypotenuse
F
H
=
3
2
+
6
2
=
3
5
The hypotenuse
F
H
=
3
2
+
6
2
=
3
5
Half perimeter of F G H is then s = 2 1 ( 3 5 + 2 3 )
Heron's formula for the area [ F G H ] = s ( s − 3 5 ) ( s − 1 0 ( s − 1 3 ) = 3 3
[ E F G H ] = [ E F H ] + [ F G H ] = 2 1 × 3 × 6 + 3 3 = 4 2
As an alternative approach...
Draw a vertical from G to the extension of E H and let the point of intersection be A , Next, draw a horizontal from G to the extension of E F and call the point of intersection B . Now let ∣ H A ∣ = x and ∣ F B ∣ = y . Then by Pythagoras we have that
( 6 + x ) 2 + y 2 = 1 3 2 ⟹ x 2 + 1 2 x + y 2 = 1 3 3 , and
x 2 + ( y + 3 ) 2 = 1 0 2 ⟹ x 2 + 6 y + y 2 = 9 1 .
Upon subtracting the second from the first of these equations we have that 1 2 x − 6 y = 4 2 ⟹ y = 2 x − 7 .
Substituting this result into x 2 + ( y + 3 ) 2 = 1 0 2 and simplifying yields that
x 2 + ( 2 x − 4 ) 2 = 1 0 0 ⟹ 5 x 2 − 1 6 x − 8 4 = ( 5 x + 1 4 ) ( x − 6 ) = 0 ,
from which we can conclude that x = 6 , (as we must have x > 0 ), and thus y = 2 x − 7 = 5 .
The green area will then be the area of rectangle E B G A minus the areas of triangles Δ H A G and Δ F B G , which comes out to
( x + 6 ) ( y + 3 ) − 2 x ( y + 3 ) − 2 y ( x + 6 ) = 1 2 × 8 − 3 × 8 − 5 × 6 = 4 2 .