Another Problem by Mark Vincent Esmeralda Mamigo...
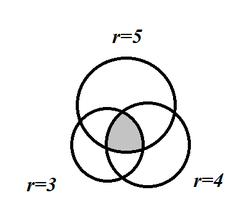We have three circles of radius 3, 4 and 5 units respectively.. Two points of the circle having the radius 5 touches the centers of circles with radius 3 and 4, and a point of circle having radius 4 touches the center of circle having radius 3.. When these three circles are overlapped, part of them in the center is thickened.. Can you find the area of that portion?? (shaded area).. Answer understood to be in square units.. Up to three decimal places if possible (to attain accuracy)..
The answer is 6.870639926.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
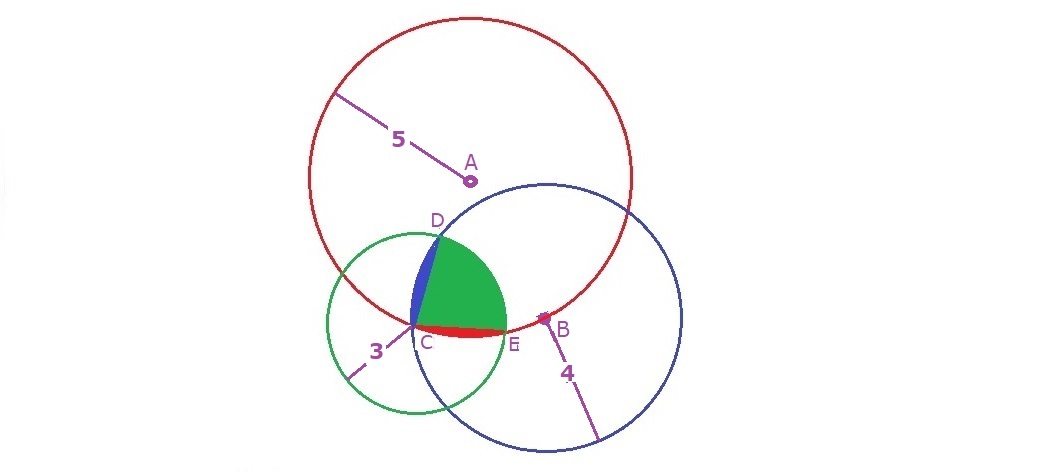
Plotting the circles in the Cartesian plane, we get these equations..
x^{2}+y^{2}=9
(x-4)^{2}+y^{2}=16
(x-2)^{2}+(y-\sqrt {21})=25
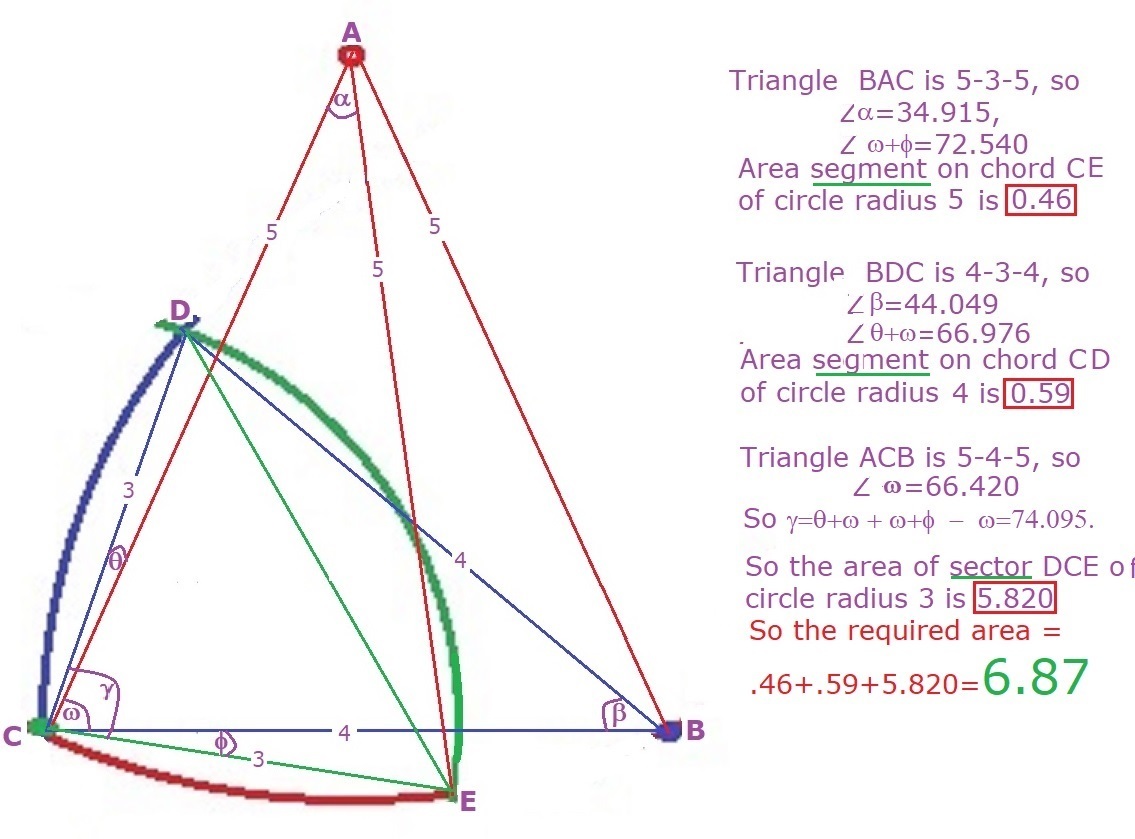
solving simultaneously for their points of intersection, we get the points.. (0,0), (2.983,-0.320), (1.125,2.781).. These three points form a triangle, so to find the area, we get their lengths which are 3.615, 3 and 3, and the area of the triangle would be 4.327799638.. Get also for the area of the sector of the circle, we have from circle with radius 3 is 1.491868422, from circle with radius 4 is 0.5881995267 and from circle with radius 5 is 1.4627723394.. Adding these portions will yield to the answer as the area of the shaded portion in the problem..